题目内容
已知函数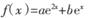 (a ,b
(a ,b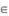 R,e为自然对数的底数),
R,e为自然对数的底数),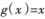 .
.
(I )当b=2时,若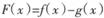 存在单调递增区间,求a的取值范围;
存在单调递增区间,求a的取值范围;
(II)当a>0 时,设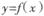 的图象C1与
的图象C1与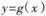 的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点
的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点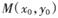 ,求证
,求证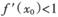 .
.
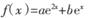 (a ,b
(a ,b R,e为自然对数的底数),
R,e为自然对数的底数),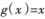 .
.(I )当b=2时,若
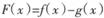 存在单调递增区间,求a的取值范围;
存在单调递增区间,求a的取值范围;(II)当a>0 时,设
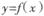 的图象C1与
的图象C1与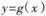 的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点
的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点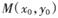 ,求证
,求证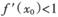 .
.(Ⅰ)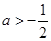 .(Ⅱ)见解析
.(Ⅱ)见解析
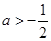 .(Ⅱ)见解析
.(Ⅱ)见解析(Ⅰ)先求出函数的导数,然后利用条件转化为方程有解问题;(Ⅱ)构造函数,利用导数法研究函数的单调性。
(Ⅰ)当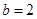 时,若
时,若 ,则
,则
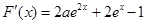 ,原命题等价于
,原命题等价于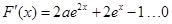 在R上有解.…2分
在R上有解.…2分
法一:当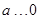 时,显然成立;
时,显然成立;
当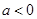 时,
时,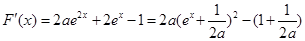
∴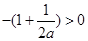 ,即
,即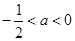 .综合所述
.综合所述 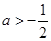 .…………………5分
.…………………5分
法二:等价于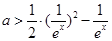 在R上有解,即∴
在R上有解,即∴ 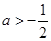 .………………5分
.………………5分
(Ⅱ)设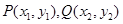 ,不妨设
,不妨设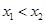 ,则
,则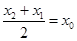 ,
,
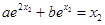 ,
,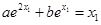 ,
,
两式相减得: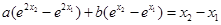 ,……………7分
,……………7分
整理得
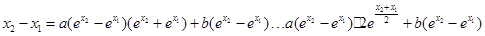
则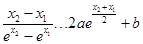 ,于是
,于是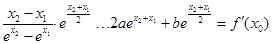 ,……9分
,……9分
而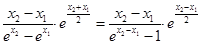
令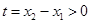 ,则设
,则设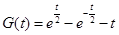 ,则
,则
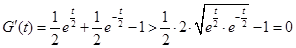 ,
,
∴ 在
在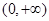 上单调递增,则
上单调递增,则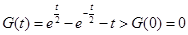 ,于是有
,于是有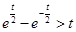 ,即
,即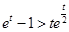 ,且
,且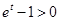 ,∴
,∴ 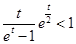 ,即
,即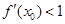 .
.
(Ⅰ)当
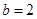 时,若
时,若 ,则
,则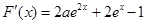 ,原命题等价于
,原命题等价于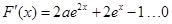 在R上有解.…2分
在R上有解.…2分法一:当
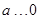 时,显然成立;
时,显然成立;当
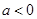 时,
时,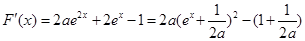
∴
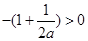 ,即
,即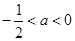 .综合所述
.综合所述 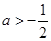 .…………………5分
.…………………5分法二:等价于
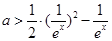 在R上有解,即∴
在R上有解,即∴ 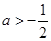 .………………5分
.………………5分(Ⅱ)设
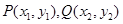 ,不妨设
,不妨设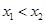 ,则
,则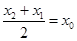 ,
,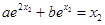 ,
,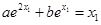 ,
,两式相减得:
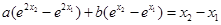 ,……………7分
,……………7分整理得
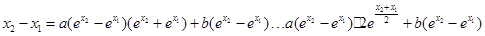
则
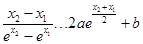 ,于是
,于是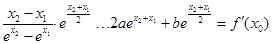 ,……9分
,……9分而
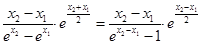
令
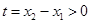 ,则设
,则设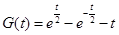 ,则
,则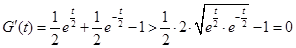 ,
,∴
 在
在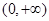 上单调递增,则
上单调递增,则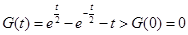 ,于是有
,于是有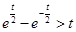 ,即
,即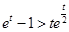 ,且
,且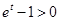 ,∴
,∴ 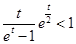 ,即
,即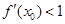 .
.
练习册系列答案
相关题目
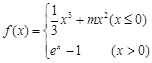
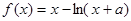 的最小值为0,其中
的最小值为0,其中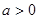 。
。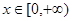 ,有
,有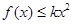 成立,求实数k的最小值
成立,求实数k的最小值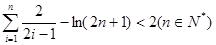
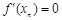 ,则
,则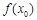 是函数
是函数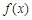 的极值
的极值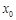 处有导数
处有导数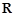 上的可导函数
上的可导函数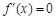 无实数解,则
无实数解,则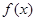 为定义在
为定义在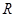 上的偶函数,当
上的偶函数,当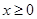 时,
时,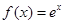 ,(其中
,(其中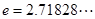 为自然对数的底数),
为自然对数的底数),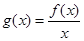 ,求
,求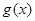 在区间
在区间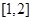 上的最大值
上的最大值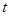 ,对任意
,对任意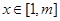 ,都有
,都有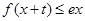 成立,求正整数
成立,求正整数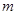 的最大值
的最大值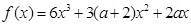 .
.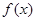 的两个极值点为
的两个极值点为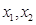 ,且
,且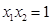 ,求实数
,求实数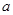 的值;
的值; 上的单调函数?若存在,求出
上的单调函数?若存在,求出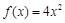 的导函数是( )
的导函数是( )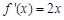
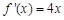

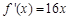
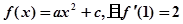 ,则a的值为 ( )
,则a的值为 ( )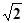
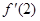 =( )
=( )