题目内容
5.直线2x+2y-1=0的倾斜角是135°.分析 利用斜率与倾斜角的关系即可得出.
解答 解:设此直线的倾斜角为θ,θ∈[0°,180°).
则tanθ=-$\frac{2}{2}$=-1,∴θ=135°.
故答案为:135°.
点评 本题考查了直线的斜率与倾斜角的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
16.设A是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点,F(c,0)是右焦点,若抛物线${y^2}=-\frac{{4{a^2}}}{c}x$的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )
| A. | [2,+∞) | B. | (1,2] | C. | (1,3] | D. | [3,+∞) |
13.已知等比数列{an}的前n项和Sn=2n-a,则数列{log2an}的前10项和等于( )
| A. | 1023 | B. | 55 | C. | 45 | D. | 35 |
20.设集合$A=\left\{{({x,y})|\frac{x^2}{4}+\frac{y^2}{16}=1}\right\}$,B={(x,y)|y=3x},则A∩B的子集的个数是( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
14.已知角φ的终边在射线$y=\sqrt{3}x(x≤0)$上,函数f(x)=cos(ωx+φ)(ω>0)图象的相邻两条对称轴之间的距离等于$\frac{π}{3}$,则$f(\frac{π}{6})$=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
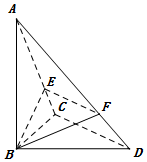 在三棱锥A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分别是AC、AD上的点,且$\frac{AE}{AC}=\frac{AF}{AD}$.
在三棱锥A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分别是AC、AD上的点,且$\frac{AE}{AC}=\frac{AF}{AD}$.