题目内容

5．若直线l1：（2a+3）x+（a-1）y+3=0与l2：（a+2）x+1（1-a）y-3=0平行，则实数a=1．

分析 讨论直线的斜率都不存在与斜率都存在时，求出两直线平行时a的值即可．

解答 解：当a=1时，两直线的斜率都不存在，
它们的方程分别是x=-1和x=$\frac{3}{2}$，显然两直线平行；
当a≠1时，两直线的斜率都存在，故有斜率相等，
∴-$\frac{2a+3}{a-1}$=-$\frac{a+2}{1-a}$，
解得a=-$\frac{5}{3}$，此时两方程为x+8y-9=0和x+8y-9=0，两直线重合；
综上，a=1，
故答案为：1．

点评 本题考查了两直线平行的条件，要注意特殊情况即直线斜率不存在以及两直线重合的情况，是基础题．

练习册系列答案
相关题目
15．圆（x-1）2+y2=4的半径为2．
16．双曲线kx2-2ky2+1=0的一个焦点为（-4，0），则实数k=$-\frac{3}{32}$．
13．设函数f（x）=logax（a＞0，且a≠1），若f（x1x2…x2013）=8，则f（x${\;}_{1}^{2}$）+f（x${\;}_{2}^{2}$+…+f（x${\;}_{2013}^{2}$）=16．
20．已知数列1，a1，a2，4成等差数列1，b1，b2，4成等比数列，则$\frac{{a}_{2}-{a}_{1}}{{b}_{2}}$的值是$\frac{\root{3}{4}}{4}$．
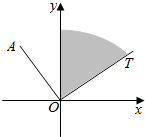10．如图所示，在直角坐标系内，射线OT落在30°角的终边上，任作一条射线OA，则射线OA落在∠yOT内的概率为$\frac{1}{6}$．
17．等比数列x，3x+3，6x+6，…的第四顶等于-24．
14．等比数列{an}中，S10=10，S20=30，求S30．
16．已知全集U=R，集合$A=\{x|y=\sqrt{\frac{4-x}{x-2}}\}，B=\{x|{x^2}-7x+12≤0\}，则A∩$（∁UB）=（　　）
A．（2，3）B．（2，4）C．（3，4]D．（2，4]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网