题目内容
已知:数列{an}的前n项和为Sn,若Sn=
,
(Ⅰ)求证:{an}是等差数列;
(Ⅱ)若a>0且a2=2a+1,S5=5(3a+1),求证:
+
+…+
<
.
| n(a1+an) |
| 2 |
(Ⅰ)求证:{an}是等差数列;
(Ⅱ)若a>0且a2=2a+1,S5=5(3a+1),求证:
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| n | ||||
(1+
|
考点:数列与不等式的综合
专题:
分析:(Ⅰ)再写一式,两式相减,即可证明{an}是等差数列;
(Ⅱ)利用数学归纳法证明.
(Ⅱ)利用数学归纳法证明.
解答:
证明:(Ⅰ)当n≥2时,Sn=
①,Sn-1=
②
①-②得:an=
-
∴2an=nan-(n-1)an-1+a1③…(2分)2an+1=(n+1)an+1-nan+a1④
④-③得:2an+1-2an=(n+1)an+1-2nan+(n-1)an-1…(3分)
∴(n-1)an+1+(n-1)an-1=2(n-1)an…(4分)
即:an+1+an-1=2an
∴{an}是等差数列;…(5分)
(Ⅱ)①当n=1时,
=
<
不等式成立,…(6分)
②假设n=k(k≥1)时,不等式成立,
即
+
+…+
<
…(7分)
那么n=k+1时,
+
+…+
+
<
+
…(8分)<
+
=
=
=
…(11分)
即n=k+1时,不等式也成立,
由①②得,不等式恒成立.…(12分)
| n(a1+an) |
| 2 |
| (n-1)(a1+an-1) |
| 2 |
①-②得:an=
| n(a1+an) |
| 2 |
| (n-1)(a1+an-1) |
| 2 |
∴2an=nan-(n-1)an-1+a1③…(2分)2an+1=(n+1)an+1-nan+a1④
④-③得:2an+1-2an=(n+1)an+1-2nan+(n-1)an-1…(3分)
∴(n-1)an+1+(n-1)an-1=2(n-1)an…(4分)
即:an+1+an-1=2an
∴{an}是等差数列;…(5分)
(Ⅱ)①当n=1时,
| 1 | ||
|
| 1 |
| (1+a)2 |
| 1 | ||||
(1+
|
②假设n=k(k≥1)时,不等式成立,
即
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| k | ||||
(1+
|
那么n=k+1时,
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| k | ||||
(1+
|
| 1 |
| [1+a(k+1)]2 |
| k | ||||
(1+
|
| 1 | ||||
(1+
|
k(1+
| ||||||
(1+
|
(k+1)(1+
| ||||||
(1+
|
| k+1 | ||||
(1+
|
即n=k+1时,不等式也成立,
由①②得,不等式恒成立.…(12分)
点评:本题考查等差数列的证明,考查数学归纳法,考查学生分析解决问题的能力,正确运用数学归纳法是关键.

练习册系列答案
相关题目
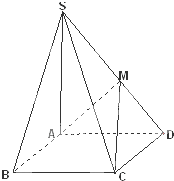 如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=2AB.
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=2AB.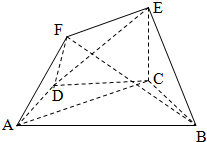 如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=