Question

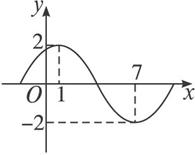
已知正弦曲线y=Asin（ωx+φ），（A＞0，ω＞0）上一个最高点的坐标是（2，），由这个最高点到相邻的最低点，曲线交x轴于（6，0）点，则这条曲线的解析式是

1. A.
   y=sin（x+）
2. B.
   y=sin（x-2）
3. C.
   y=sin（x+2）
4. D.
   y=sin（x-）

Answer 1

A
分析：由三角函数图象和性质，曲线y=Asin（ωx+φ）的最高点求A，再由最高点与相邻的平衡点求最小正周期T，进一步求得ω，最后通过特殊点求φ，则问题解决．
解答：由曲线y=Asin（ωx+φ）的一个最高点是（2，），得A=，
又最高点（2， ）到相邻的最低点间，曲线与x轴交于点（6，0），
则 =6-2=4，即T=16，所以ω==．
此时y=sin（ x+φ），
将x=2，y=代入得φ=，
所以这条曲线的解析式为
故选A．
点评：本题主要考查三角函数图象、性质．由曲线y=Asin（ωx+φ）的部分信息求函数y=Asin（ωx+φ）的解析式一般先确定A再确定T，通过特殊点求φ．