题目内容
已知正弦曲线f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一部分图象如图所示.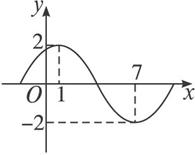
(1)求函数f(x)的解析式;
(2)求证:x=1是y=f(x)的对称轴;
(3)求y=f(x)关于x=2对称的图象y=g(x)的解析式.
(1)解:因为f(x)在x=1时有最大值2,在x=7时有最小值-2,又T=2(7-1)=12,
所以ω=![]() =
=![]() ,A=2,
,A=2,
所以f(x)=2sin(![]() +φ).
+φ).
又图象过(1,2)点,
所以2sin(![]() +φ)=2.
+φ)=2.
结合0<φ<π,
可得φ=![]() ,
,
所以f(x)=2sin(![]() x+
x+![]() ).
).
(2)证明:因为f(1+t)=2sin[![]() (1+t)+
(1+t)+![]() ]
]
=2sin(![]() +
+![]() t)=2cos(
t)=2cos(![]() t),
t),
f(1-t)=2sin[![]() (1-t)+
(1-t)+![]() ]
]
=2sin(![]() -
-![]() t)=2cos(
t)=2cos(![]() t),
t),
所以f(1+t)=f(1-t).
所以x=1是y=2sin(![]() x+
x+![]() )图象的对称轴.
)图象的对称轴.
(3)解:与y=f(x)关于x=2对称的函数为y=f(4-x),
所以g(x)=f(4-x)=2sin[![]() (4-x)+
(4-x)+![]() ]
]
=2sin(![]() x),即g(x)=2sin(
x),即g(x)=2sin(![]() x).
x).

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 -
- )
)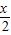 -
-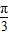 )
)