题目内容
(本题满分16分)
已知函数 (
( ∈R且
∈R且 ),
), .
.
(Ⅰ)若 ,且函数
,且函数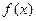 的值域为[0, +
的值域为[0, + ),求
),求 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2 , 2 ]时, 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
(Ⅲ)设 ,
, , 且
, 且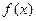 是偶函数,判断
是偶函数,判断 能否大于零?
能否大于零?
(Ⅰ)
(Ⅱ) 或
或
(Ⅲ) 
解析解:(Ⅰ) ………………………………1分
………………………………1分
∵函数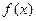 的值域为[0, +
的值域为[0, + )
)
∴ 且△=
且△= ∴
∴ …………3分
…………3分
∴ ……………………………………4分
……………………………………4分
(Ⅱ) ………………………6分
………………………6分
在定义域x∈[-2 , 2 ]上是单调函数,对称轴为 ………………8分
………………8分
∴ 或
或
即 或
或 ……………………………………10分
……………………………………10分
(Ⅲ)∵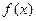 是偶函数 ∴
是偶函数 ∴
∴
∴ ∴
∴ …………12分
…………12分
∴ …………………………………………13分
…………………………………………13分
∵ 不妨设
不妨设 , 则
, 则 ,
, ,
,
∴
 …………15分
…………15分
∵ ,
, ,
,
∴ ……………………16分
……………………16分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在
在 上为增函数.
上为增函数. ,若
,若 能表示成一个奇函数
能表示成一个奇函数 和一个偶函数
和一个偶函数 的和.
的和. 上都是减函数,求
上都是减函数,求 的取值范围.
的取值范围. (a、b、c是常数)是奇函数,且满足
(a、b、c是常数)是奇函数,且满足 .
. )上的单调性并证明.
)上的单调性并证明. ,每人每年可创利10万元.据评估,在经营条件不变的前提下,若裁员x人,则留岗职员每人每年多创利0.1x万元,但公司需付下岗职员每人每年4万元的生活费,并且该公司正常运转情况下,所裁人数不超过50人,为获得最大的经济效益,该公司应裁员多少人?
,每人每年可创利10万元.据评估,在经营条件不变的前提下,若裁员x人,则留岗职员每人每年多创利0.1x万元,但公司需付下岗职员每人每年4万元的生活费,并且该公司正常运转情况下,所裁人数不超过50人,为获得最大的经济效益,该公司应裁员多少人? 的时候小白鼠将死亡.但注射某种药物,将可杀死此时其体内该病毒细胞的
的时候小白鼠将死亡.但注射某种药物,将可杀死此时其体内该病毒细胞的 .
.
 ,
, )
) 的单调区间及极值
的单调区间及极值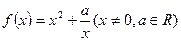
 的奇偶性;
的奇偶性; 是增函数,求实数
是增函数,求实数 的 取值范围。
的 取值范围。 000元的电视机共3600台,每批都购入x台
000元的电视机共3600台,每批都购入x台 ,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比。若每批购入400台,则全年需用去运费和保管费43600元。现在全年只有24000元资金用于支付运费和保管费,请问能否恰
,且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比。若每批购入400台,则全年需用去运费和保管费43600元。现在全年只有24000元资金用于支付运费和保管费,请问能否恰 当安排每批进货的数量,使资金够用?写出你的结论并说明理由
当安排每批进货的数量,使资金够用?写出你的结论并说明理由