题目内容
(本小题共14分)
已知函数![]() .
.![]() .
.
(I)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程(
处的切线方程(![]() );
);
(II)求函数![]() 的单调区间.
的单调区间.
(共14分)
解:(I)当![]() 时,
时,![]() ,
,![]() , ………………………2分
, ………………………2分
所以![]() ,
,![]() , ………………………4分
, ………………………4分
所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .………………………5分
.………………………5分
(II)函数![]() 的定义域为
的定义域为![]()
![]() ,…………………………6分
,…………………………6分
①当![]() 时,
时,![]() ,在
,在![]() 上
上![]() ,在
,在![]() 上
上![]()
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上递减; ……………………………………………8分
上递减; ……………………………………………8分
②当![]() 时,在
时,在![]() 和
和![]() 上
上![]() ,在
,在![]() 上
上![]()
所以![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上递减;………………………10分
上递减;………………………10分
③当![]() 时,在
时,在![]() 上
上![]() 且仅有
且仅有![]() ,
,
所以![]() 在
在![]() 上单调递增; ……………………………………………12分
上单调递增; ……………………………………………12分
④当![]() 时,在
时,在![]() 和
和![]() 上
上![]() ,在
,在![]() 上
上![]()
所以![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上递减……………………………14分
上递减……………………………14分

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是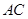 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.