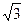题目内容
如图所示的一组图形为某一四棱锥S—ABCD的侧面与底面,

(1)指出各侧棱长;
(2)在(1)的条件下,过A且垂直于SC的平面分别交于SB、SC、SD于E、F、G.
求(1)(2)的条件下,求二面角A—SC—B的大小.

(1)指出各侧棱长;
(2)在(1)的条件下,过A且垂直于SC的平面分别交于SB、SC、SD于E、F、G.
求(1)(2)的条件下,求二面角A—SC—B的大小.
(1)SA= (2)arcsin
(2)arcsin
 (2)arcsin
(2)arcsin
(1)SA=
(2)∵SC⊥平面AEFG,A又AE 平面AEFG,∴AE⊥SC,∵SA⊥平面BD,又BC
平面AEFG,∴AE⊥SC,∵SA⊥平面BD,又BC 平面BD,∴SA⊥BC.又AB⊥BC,SA∩AB="A," ∴BC⊥平面SBC,∴AF在平面SBC上射影为EF.
平面BD,∴SA⊥BC.又AB⊥BC,SA∩AB="A," ∴BC⊥平面SBC,∴AF在平面SBC上射影为EF.
由三垂线定理得∠AFE为二面角A—SC—B的平面角,易得AF=
∵AE⊥平面SBC,又SB 平面SBC, ∴AE⊥SB.
平面SBC, ∴AE⊥SB.
∴AE= A—SC—B的大小为arcsin
A—SC—B的大小为arcsin

(2)∵SC⊥平面AEFG,A又AE
 平面AEFG,∴AE⊥SC,∵SA⊥平面BD,又BC
平面AEFG,∴AE⊥SC,∵SA⊥平面BD,又BC 平面BD,∴SA⊥BC.又AB⊥BC,SA∩AB="A," ∴BC⊥平面SBC,∴AF在平面SBC上射影为EF.
平面BD,∴SA⊥BC.又AB⊥BC,SA∩AB="A," ∴BC⊥平面SBC,∴AF在平面SBC上射影为EF.由三垂线定理得∠AFE为二面角A—SC—B的平面角,易得AF=

∵AE⊥平面SBC,又SB
 平面SBC, ∴AE⊥SB.
平面SBC, ∴AE⊥SB.∴AE=
 A—SC—B的大小为arcsin
A—SC—B的大小为arcsin

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 与
与 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面 平面
平面 ,
, 平面
平面
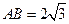 .
.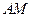 与平面
与平面 与平面
与平面 如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为
如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为 的等腰三角形,求二面角V-AB-C的大小.
的等腰三角形,求二面角V-AB-C的大小.  π,π)
π,π) π,π)
π,π) )
)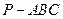 中,
中,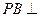 底面
底面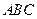 于
于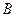 ,
,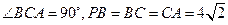 ,点
,点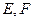 分别是
分别是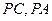 的中点,求二面角
的中点,求二面角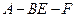 的余弦值.
的余弦值.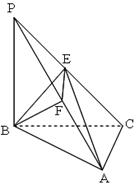
 正切值;
正切值;
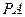 、
、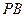 、
、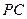 是从空间一点
是从空间一点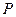 出发的三条射线,若
出发的三条射线,若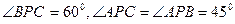 ,求二面角
,求二面角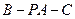 的大小.
的大小.
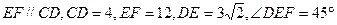 ,DA、CB都垂直于EF,且垂足分别为A,B,将梯形沿DA、CB折起,使E、F重合于点P,点M在AB上,且
,DA、CB都垂直于EF,且垂足分别为A,B,将梯形沿DA、CB折起,使E、F重合于点P,点M在AB上,且 。
。
 B
B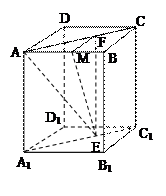 A.
A.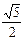 B.
B.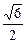 C.
C.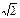 D.
D.