题目内容
已知函数f(x)=
在R上为单调函数,求实数a的取值范围.
|
考点:函数单调性的性质
专题:函数的性质及应用
分析:分当x<0、当x>0两种情况,分别考查导数的符号,求得a的范围,综合可得结论.
解答:
解:当x<0时,f′(x)=x(2-ax)e-ax,
当x>0时,f′(x)=
=
.
若f(x)在R上为单调递增函数,则当x>0时,f′(x)=
>0,显然a∈∅.
若f(x)在R上为单调递减函数,则
当x>0时,f′(x)=
<0,即a>-x2-2x,所以a≥0.
当x<0时,f′(x)=x(2-ax)e-ax<0,即ax-2<0,所以a≥0.
当x=0时,0≥a-1,即a≤1.
综上可得0≤a≤1.
当x>0时,f′(x)=
| -2x(x+1)-(a-x2) |
| (x+1)2 |
| -x2-2x-a |
| (x+1)2 |
若f(x)在R上为单调递增函数,则当x>0时,f′(x)=
| -x2-2x-a |
| (x+1)2 |
若f(x)在R上为单调递减函数,则
当x>0时,f′(x)=
| -x2-2x-a |
| (x+1)2 |
当x<0时,f′(x)=x(2-ax)e-ax<0,即ax-2<0,所以a≥0.
当x=0时,0≥a-1,即a≤1.
综上可得0≤a≤1.
点评:本题主要考查利用导数研究函数的单调性,函数的单调性的定义、性质,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
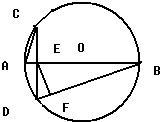 如图,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F.
如图,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F.