题目内容
11.若幂函数y=xa的图象过点(2,$\frac{1}{2}$),则a=-1.分析 根据题意,将点(2,$\frac{1}{2}$)的坐标代入y=xa中,可得$\frac{1}{2}$=2a,解可得a的值,即可得答案.
解答 解:根据题意,点(2,$\frac{1}{2}$)在幂函数y=xa的图象上,
则有$\frac{1}{2}$=2a,
解可得a=-1;
故答案为:-1.
点评 本题考查幂函数解析式的计算,注意幂函数与指数函数的区别.

练习册系列答案
相关题目
2.抛物线4y=x2的焦点到准线的距离为( )
| A. | 2 | B. | 4 | C. | $\frac{1}{8}$ | D. | $\frac{1}{2}$ |
19.若cos($\frac{π}{6}-x$)=-$\frac{1}{3}$,则cos($2x+\frac{2π}{3}$)=( )
| A. | $±\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{4\sqrt{2}}{9}$ | D. | $\frac{7}{9}$ |
3.已知a=log32,b=log2$\frac{1}{3}$,c=2${\;}^{\frac{1}{3}}$,则( )
| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | a>b>c |
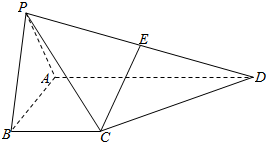 如图,在四棱锥P-ABCD 中,侧面PAB 为正三角形,侧面PAB⊥底面ABCD,E 为PD 的中点,AB⊥AD,BC∥AD,且AB=BC=$\frac{1}{2}$AD=2.
如图,在四棱锥P-ABCD 中,侧面PAB 为正三角形,侧面PAB⊥底面ABCD,E 为PD 的中点,AB⊥AD,BC∥AD,且AB=BC=$\frac{1}{2}$AD=2.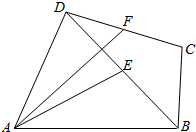 四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.
四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.