题目内容
叙述并证明直线与平面垂直的判定定理.
解:定理叙述:
若一条直线垂直于一个平面内两条相交直线,则该直线与此平面垂直。
证明:已知:直线, ,
,

求证:

证明:设p是平面 内任意一条直线,则只需证
内任意一条直线,则只需证
设直线 的方向向量分别是
的方向向量分别是
只需证



 与
与 不共线
不共线 直线
直线 在同一平面
在同一平面 内,
内,
根据平面向量基本定理存在实数 使得
使得
则


所以直线 垂直于平面
垂直于平面
解析

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
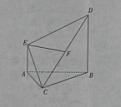
在空间直角坐标系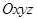 中,已知
中,已知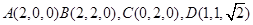 .若
.若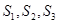 分别是三棱锥
分别是三棱锥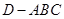 在
在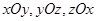 坐标平面上的正投影图形的面积,则( )
坐标平面上的正投影图形的面积,则( )
A.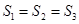 | B.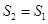 且 且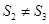 |
C.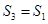 且 且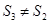 | D.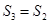 且 且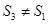 |
 中,侧棱
中,侧棱 ,点
,点 是
是 的中点,
的中点, .
. ∥平面
∥平面 ;
; 为棱
为棱 的中点,试证明:
的中点,试证明: .
.
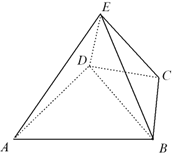
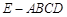 是四棱锥,△
是四棱锥,△ 为正三角形,
为正三角形, .
.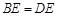 ;
;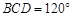 ,M为线段AE的中点,求证:
,M为线段AE的中点,求证: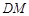 ∥平面
∥平面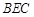 .
.
 中,设
中,设 ,
, ,
, 上存在点
上存在点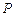 满足
满足
 平面
平面 ,求实数
,求实数 的取值范围
的取值范围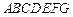 中,
中,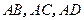 两两垂直,平面
两两垂直,平面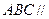 平面
平面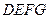 ,
,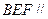 平面
平面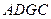 ,
, .
.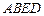 是正方形;
是正方形; 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?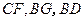 ,求证:
,求证: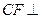 平面
平面 .
.
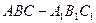 中,底面
中,底面 是边长为2的正三角形,侧棱长为3,且侧棱
是边长为2的正三角形,侧棱长为3,且侧棱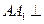 面
面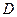 是
是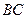 的中点.
的中点.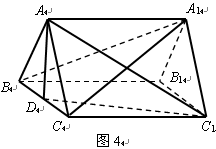
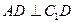 ;
;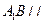 平面
平面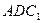 .
.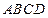 中,
中, ,
,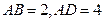 将
将 沿
沿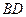 折起到
折起到 的位置,使平面
的位置,使平面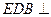 平面
平面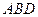
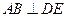 (Ⅱ)求三棱锥
(Ⅱ)求三棱锥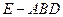 的侧面积。
的侧面积。