题目内容
(本小题满分16分)
如图,多面体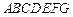 中,
中,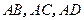 两两垂直,平面
两两垂直,平面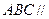 平面
平面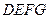 ,
,
平面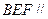 平面
平面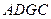 ,
, .
.
(1)证明四边形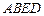 是正方形;
是正方形;
(2)判断点 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?
(3)连结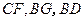 ,求证:
,求证: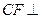 平面
平面 .
.
证明:(1)
…………..2分
同理 ,……..3分
,……..3分
则四边形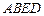 是平行四边形.
是平行四边形.
又
 四边形
四边形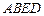 是正方形. ……..4分
是正方形. ……..4分
(2) 取 中点
中点 ,连接
,连接 .
.
在梯形 中,
中,  且
且 .
.
又 且
且 ,
,
 且
且 .……………………..5分
.……………………..5分 四边形
四边形 为平行四边形, ……………………..6分
为平行四边形, ……………………..6分
 . ……………………..7分
. ……………………..7分
在梯形 中,
中,

 , ……………………..9分
, ……………………..9分
 四点共面. …………………….10分
四点共面. …………………….10分
(3)同(1)中证明方法知四边形BFGC为平行四边形.
且有 ,从而
,从而 ,
, . ……………………..12分
. ……………………..12分
又 故
故 ,而
,而 ,
,
故四边形BFGC为菱形, . ……………………..14分
. ……………………..14分
又由 知
知 .
.
正方形 中,
中, ,故
,故 .
. . ……………………..16分
. ……………………..16分
解析

练习册系列答案
相关题目
若{a,b,c}为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
| A.a,a+b,a-b | B.b,a+b,a-b |
| C.c,a+b,a-b | D.a+b,a-b,a+2b |
 被一平面所截,截面
被一平面所截,截面 是一个平行四边形.求证:
是一个平行四边形.求证: ;
;
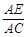 =
= =λ (0<λ<1).
=λ (0<λ<1).

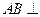 侧面BB1C1C,已知AB=BC=1,BB1=2,
侧面BB1C1C,已知AB=BC=1,BB1=2,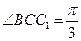 ,E为CC1的中点。
,E为CC1的中点。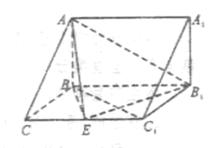
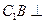 平面ABC;
平面ABC; B。
B。
 FE交AP于E,交DP于F.求证:四边形BCFE是梯形.
FE交AP于E,交DP于F.求证:四边形BCFE是梯形.