题目内容
如图已知四边形ABCD是正方形,BE∥AC,AC=CE,EC的延长线交BA的延长线于F.求证:![]() =
=![]() .
.
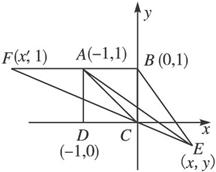
思路分析:可以建立直角坐标系,要证明|![]() |=|
|=|![]() |,只要求出A与E、F点的坐标即可.
|,只要求出A与E、F点的坐标即可.
证明:如题图,以正方形ABCD的CD所在直线为x轴,以C点为原点建立直角坐标系.设正方形的边长为1,则A、B的坐标分别为(-1,1),(0,1)若E点的坐标为(x,y),则![]() =(x,y-1),
=(x,y-1),![]() =(1,-1).
=(1,-1).
∵![]() ∥
∥![]() ,
,
即x+y=1①
又∵|![]() |=|
|=|![]() |.
|.
∴x2+y2=2.②
由①②得E点的坐标为(![]() ,
,![]() ).
).
如果设F点的坐标为(x′,1),由![]() =(x′,1)与
=(x′,1)与![]() =(
=(![]() ,
,![]() )共线,得
)共线,得![]() x′-
x′-![]() =0,解得
=0,解得
x′=-(2+![]() ),即点F的坐标为(-2-
),即点F的坐标为(-2-![]() ,1).
,1).
∵![]() =(-1-
=(-1-![]() ,0),
,0),![]() =(
=(![]() ,
,![]() ).
).
∴|![]() |=1+
|=1+![]() =|
=|![]() |.即AF=AE.
|.即AF=AE.
温馨提示
由于向量同时具备数、形的特点,能够顺利实现形、数的相互转化,因此在解决几何问题时常常能够化严格的逻辑推理为简单的计算.特别是在触及线段的平行或垂直问题时,向量便更有用武之地了.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知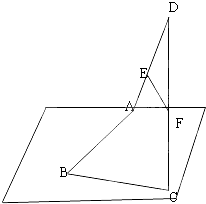 已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC.
已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC. 如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
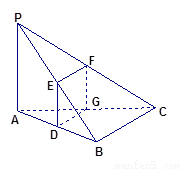 如图,已知三棱锥P—ABC中,PA⊥平面ABC,设AB、PB、PC的中点分别为D、E、F,
如图,已知三棱锥P—ABC中,PA⊥平面ABC,设AB、PB、PC的中点分别为D、E、F,