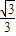题目内容
 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知| AM |
| c |
| AN |
| d |
| c |
| d |
| AB |
| AD |
(2)在△ABC中,若
| AB |
| a |
| AC |
| b |
| AP |
| AQ |
| AS |
| 3 |
| 2 |
| a |
| b |
分析:(1)由M、N分别为DC、BC的中点,则
=
,我们易根据向量加法的三角形法则,用
、
表示
和
.
(2)由
=
,
=
,我们易将向量
,
,
,用
,
表示,利用向量加减法的运算法则,易得到
+
+
=
(
+
).
| DM |
| 1 |
| 2 |
| AB |
| c |
| d |
| AB |
| AD |
(2)由
| AB |
| a |
| AC |
| b |
| AP |
| AQ |
| AS |
| a |
| b |
| AP |
| AQ |
| AS |
| 3 |
| 2 |
| a |
| b |
解答:解:(1)由
=
,
=
∴
=
+
,
=
+
即
解得:
=
-
=
-
(7分)
(2)证明:
=
+
,
=
+
,
=
+
∴
+
+
=
(
+
),
∴
+
+
=
(
+
)(14分)
| DM |
| 1 |
| 2 |
| AB |
| BN |
| 1 |
| 2 |
| AD |
∴
| c |
| AD |
| DM |
| d |
| AB |
| BN |
即
|
解得:
| AB |
| 4 |
| 3 |
| d |
| 2 |
| 3 |
| c |
| AD |
| 4 |
| 3 |
| c |
| 2 |
| 3 |
| d |
(2)证明:
| AP |
| 3 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| AQ |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
| AC |
| 1 |
| 4 |
| AB |
| 3 |
| 4 |
| AC |
∴
| AP |
| AQ |
| AC |
| 3 |
| 2 |
| AB |
| AC |
∴
| AP |
| AQ |
| AC |
| 3 |
| 2 |
| a |
| b |
点评:本题考查的知识点是向量加减混合运算及其几何意义,利用向量加减法的三角形法则,及数乘向量运算法则,将平面内任一向量分解为用基底向量表示的形式,是解答本题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 AB,则
AB,则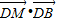 •等于( )
•等于( )
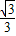
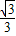
 AB,则
AB,则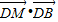 •等于( )
•等于( )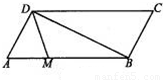
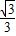
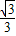
 AB,则
AB,则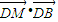 •等于( )
•等于( )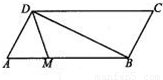
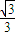
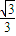
 AB,则
AB,则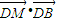 •等于( )
•等于( )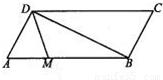
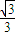

 AB,则
AB,则 •等于( )
•等于( )