题目内容
若a=
，b=
，c=
．则
- A.b＞a＞c
- B.b＞c＞a
- C.a＞b＞c
- D.a＞c＞6
C
分析：依据对数的性质，指数的性质，分别确定a、b、c数值的大小，借助于中间量“0”，“1”比较即可得到答案．
解答：因为a==
；
b==2-1.5．
∴a＞b＞0；
∵c=log2
=log2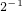
=-1＜0；
∴a＞b＞c．
故选：C．
点评：本题主要考查数的大小比较．通常数的大小比较常将数与中间量“0”，“1”比较．
分析：依据对数的性质，指数的性质，分别确定a、b、c数值的大小，借助于中间量“0”，“1”比较即可得到答案．
解答：因为a=
=；b=
=2-1.5．∴a＞b＞0；
∵c=log2
=log2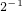=-1＜0；∴a＞b＞c．
故选：C．
点评：本题主要考查数的大小比较．通常数的大小比较常将数与中间量“0”，“1”比较．
练习册系列答案
53随堂测系列答案
相关题目
已知：函数f(x)=
，若a，b，c均不相等，且f（a）=f（b）=f（c），则a•b•c的取值范围是（ ）
|
| A、（0，9） |
| B、（2，9） |
| C、（9，11） |
| D、（2，11） |
若A，B，C是直线存在实数x使得x2
+x
+
=
，实数x为（ ）
| OA |
| OB |
| BC |
| 0 |
| A、-1 | ||||
| B、0 | ||||
C、
| ||||
D、
|