题目内容
15.直线l1的斜率k1=$\frac{1}{2}$,直线l2的倾斜角是直线l1的倾斜角的2倍,则直线l2的斜率k2=( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
分析 设出l1的斜率,根据二倍角公式求出直线l2的斜率即可.
解答 解:直线l1的斜率k1=$\frac{1}{2}$,设倾斜角是α,
直线l2的倾斜角是直线l1的倾斜角的2倍,
故只需l2的倾斜角是2α,
则直线l2的斜率k2=tan2α=$\frac{2tanα}{1{-tan}^{2}α}$=$\frac{1}{1-\frac{1}{4}}$=$\frac{4}{3}$,
故选:C.
点评 本题考查了求直线的斜率问题,考查二倍角公式,是一道基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
7.袋中装有6个红球和4个白球,不放回地一次摸出一个,在第一次摸出红球的条件下,第二次摸到红球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{5}{9}$ |
19.直线x-$\sqrt{3}$y+1=0的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
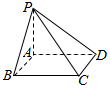 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AB=1,当直线PD与平面PBC所成角的正弦值最大时,该几何体的外接球的体积为$\frac{\sqrt{3}π}{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AB=1,当直线PD与平面PBC所成角的正弦值最大时,该几何体的外接球的体积为$\frac{\sqrt{3}π}{2}$.