题目内容
1.定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M≥0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的一个上界,已知函数f(x)=1+a($\frac{1}{2}$)x+($\frac{1}{4}$)x,g(x)=log${\;}_{\frac{1}{2}}$$\frac{1+x}{x-1}$.(1)求函数g(x)在区间[$\frac{5}{3}$,3]上的所有上界构成的集合;
(2)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围.
分析 (1)根据函数单调性的性质求出函数g(x)在区间[$\frac{5}{3}$,3]上的取值范围,结合上界的定义进行求解即可.
(2)由|f(x)|≤3在[1,+∞)上恒成立,设$t={({\frac{1}{2}})^x}$,t∈(0,1],由-3≤f(x)≤3,得-3≤1+at+t2≤3,$-({t+\frac{4}{t}})≤a≤\frac{2}{t}-t$在(0,1]上恒成立.由此入手,能够求出实数a的取值范围.
解答 解:(1)t=$\frac{1+x}{x-1}$=$\frac{x-1+2}{x-1}$=1+$\frac{2}{x-1}$,在$\frac{5}{3}$≤x≤3上为减函数,
∴2≤t≤4,
则log${\;}_{\frac{1}{2}}$4≤g(x)≤log${\;}_{\frac{1}{2}}$2,
即-2≤g(x)≤-1,
则|g(x)|≤2,
即M≥2,
即函数g(x)在区间[$\frac{5}{3}$,3]上的所有上界构成的集合为[2,+∞).
(2)由题意知,|f(x)|≤3在[0,+∞)上恒成立
设$t={({\frac{1}{2}})^x}$,t∈(0,1],由-3≤f(x)≤3,得-3≤1+at+t2≤3
∴$-({t+\frac{4}{t}})≤a≤\frac{2}{t}-t$在(0,1]上恒成立…(6分)
设$h(t)=-t-\frac{4}{t}$,$p(t)=\frac{2}{t}-t$,h(t)在(0,1]上递增;p(t)在(0,1]上递减,h(t)在(0,1]上的最大值为h(1)=-5;p(t)在(0,1]上的最小值为p(1)=1,…(9分)
所以实数a的取值范围为[-5,1].…(10分)
点评 本题考查函数的应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,正确理解新定义,合理地进行等价转化是解决本题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -$\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
| A. | -$\sqrt{3}$ | B. | -1 | C. | 0 | D. | 1 |
| A. | a>0 | B. | a>1 | C. | a<0 | D. | 0<a<1 |
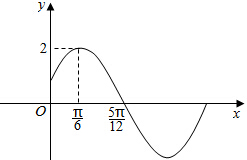 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.