题目内容
若函数f（x）=mx2+（m-1）x+m有零点，则实数m的取值范围______．
①若m=0，则f（x）=-x，
它的零点为0∉，
故m=0符合题意，
②若m≠0，
函数f（x）=mx2+（m-1）x+m有零点，
必有△=（m-1）2-4m2≥0?-1≤m≤
，且m≠0，
综上实数m的取值范围为：[-1，
]
故答案为：[-1，
]．
它的零点为0∉，
故m=0符合题意，
②若m≠0，
函数f（x）=mx2+（m-1）x+m有零点，
必有△=（m-1）2-4m2≥0?-1≤m≤
| 1 |
| 3 |
综上实数m的取值范围为：[-1，
| 1 |
| 3 |
故答案为：[-1，
| 1 |
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
和圆x2+y2=n2相切，其中m，n∈N，0＜|m-n|≤1，若函数f（x）=mx+1-n的零点x∈（k，k+1）k∈Z，则k= ．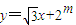
和圆x2+y2=n2相切，其中m，n∈N，0＜|m-n|≤1，若函数f（x）=mx+1-n的零点x∈（k，k+1）k∈Z，则k= ．