若i=b-i.其中a.b∈R.i是虚数单位.则复数z=a+bi的模等于( )A．0B．$\sqrt{2}$C．5D．$\sqrt{5}$ 题目和参考答案——青夏教育精英家教网—

题目内容

14．若（a-2i）i=b-i，其中a，b∈R，i是虚数单位，则复数z=a+bi的模等于（　　）

A．

B．

$\sqrt{2}$

C．

D．

$\sqrt{5}$

分析利用复数的运算法则、模的计算公式即可得出．

解答解：（a-2i）i=b-i，其中a，b∈R，i是虚数单位，
∴2+ai=b-i，可得b=2，a=-1．
则复数z=-1+2i的模=$\sqrt{（-1）^{2}+{2}^{2}}$=$\sqrt{5}$．
故选：D．

点评本题考查了复数的运算法则、模的计算公式，考查了推理能力与计算能力，属于基础题．

练习册系列答案

1．已知复数z=$\frac{4-3i}{6+8i}$（i是虚数单位），则|z|=（　　）

2．证明：函数f（x）=cos²x+cos²（x+$\frac{π}{3}$）+cos²（x-$\frac{π}{3}$）是常数函数．

9．设直线x=m分别交函数$y=sinx、y=sin（x+\frac{π}{2}）$的图象于M、N、两点，则M、N距离的最大值为（　　）

19．为了加强中国传统文化教育，某市举行了中学生成语大赛．高中组和初中组参赛选手按成绩分为A、B等级，随机从中抽取了100名选手进行调查，统计如下：
（Ⅰ）根据已知条件完成下面的2×2列联表，据此资料你能否在犯错误概率不超过0.05的前提下认为选手成绩“优秀”与文化程度有关？

	优秀	合格	合计
高中组	45		55
初中组		15
合计

（Ⅱ）若参赛选手共2万人，用频率估计概率，试估计其中A等级的选手人数；
（Ⅲ）若6名选手中，A等级的4人，B等级的2人，从这6名选手中依次不放回的取出两名选手，求取出的两名选手皆为A等级的概率．
注：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．

P（K²＞K₀）	0.10	0.05	0.005
K₀	2.706	3.841	7.879

6．

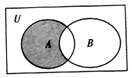若全集U、集合A、集合B及其关系用韦恩图表示如图所示，则图中阴影表示的集合为（　　）

3．若点A（x，1），B（2，y）均在第一象限，且$\overrightarrow{OA}$•$\overrightarrow{OB}$=1，则$\frac{1}{x}$+$\frac{2}{y}$的最小值为（（　　）

4．执行如图所示的程序框图，若输入m=3，n=4，则输出a=（　　）

试题分类