题目内容
 已知
已知 、
、 是两个不共线的非零向量.
是两个不共线的非零向量.
(1)设 ,
,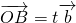 (t∈R),
(t∈R),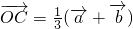 ,当A、B、C三点共线时,求t的值.
,当A、B、C三点共线时,求t的值.
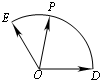
(2)如图,若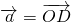 ,
,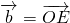 ,
, 与
与 夹角为120°,|
夹角为120°,| |=|
|=| |=1,点P是以O为圆心的圆弧
|=1,点P是以O为圆心的圆弧 上一动点,设
上一动点,设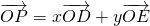 (x,y∈R),求x+y的最大值.
(x,y∈R),求x+y的最大值.
解:(1)由题意,A、B、C三点共线,可设 ,(2分)
,(2分)
∵ ,
,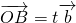 (t∈R),
(t∈R),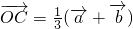 ,
,
∴ ,
, ,
,
∴ =
=
∴k=-3,t= .(6分)
.(6分)
(2)以O为原点,OD为x轴建立直角坐标系,则D(1,0),E(- ,
, ).
).
设∠POD=α(0≤α ),则P(cosα,sinα),由
),则P(cosα,sinα),由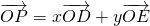 ,得cosα=x-
,得cosα=x- y,sinα=
y,sinα= ,于是y=
,于是y= ,x=cosα+
,x=cosα+ ,(10分)
,(10分)
于是x+y=cosα+ =2sin(α+
=2sin(α+ ),
),
故当α= 时,x+y的最大值为2.(14分)
时,x+y的最大值为2.(14分)
分析:(1)利用向量共线定理,及已知向量建立等式,利用平面向量基本定理,即可得到结论;
(2)建立坐标系,用三角函数确定x+y,再利用辅助角公式,即可得到结论.
点评:本题考查向量知识的综合运用,考查三角函数知识,解题的关键是掌握向量共线定理,正确运用三角函数知识,属于中档题.
 ,(2分)
,(2分)∵
 ,
,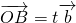 (t∈R),
(t∈R),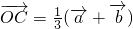 ,
,∴
 ,
, ,
,
∴
 =
=
∴k=-3,t=
 .(6分)
.(6分)(2)以O为原点,OD为x轴建立直角坐标系,则D(1,0),E(-
 ,
, ).
).设∠POD=α(0≤α
 ),则P(cosα,sinα),由
),则P(cosα,sinα),由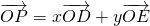 ,得cosα=x-
,得cosα=x- y,sinα=
y,sinα= ,于是y=
,于是y= ,x=cosα+
,x=cosα+ ,(10分)
,(10分)于是x+y=cosα+
 =2sin(α+
=2sin(α+ ),
),故当α=
 时,x+y的最大值为2.(14分)
时,x+y的最大值为2.(14分)分析:(1)利用向量共线定理,及已知向量建立等式,利用平面向量基本定理,即可得到结论;
(2)建立坐标系,用三角函数确定x+y,再利用辅助角公式,即可得到结论.
点评:本题考查向量知识的综合运用,考查三角函数知识,解题的关键是掌握向量共线定理,正确运用三角函数知识,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 已知
已知 、
、 是两个不共线的向量,O是同一平面内的一个定点,
是两个不共线的向量,O是同一平面内的一个定点, ,则以下结论中,错误的是
,则以下结论中,错误的是 .
.
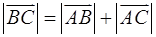 .
D.以上选项A、B、C不全对
.
D.以上选项A、B、C不全对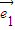 ,
,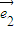 是两个不共线的单位向量,向量
是两个不共线的单位向量,向量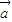 =3
=3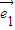 -
-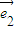 ,
, =t
=t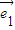 +2
+2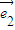 ,且
,且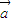 ∥
∥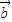 ,则t=( )
,则t=( )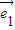 、
、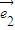 是两个不共线的平面向量,向量
是两个不共线的平面向量,向量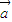 =2
=2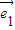 -
-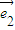 ,
,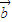 =
=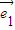 +λ
+λ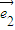 (λ∈R),若
(λ∈R),若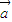 ∥
∥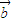 ,则λ= .
,则λ= .