题目内容
设a为正实数,记函数f(x)=a
-
-
的最大值为g(a).
(1)设t=
+
,试把f(x)表示为t的函数m(t);
(2)求g(a);
(3)问是否存在大于
的正实数a满足g(a)=g(
)?若存在,求出所有满足条件的a值;若不存在,说明理由.
| 1-x2 |
| 1+x |
| 1-x |
(1)设t=
| 1+x |
| 1-x |
(2)求g(a);
(3)问是否存在大于
| 2 |
| 1 |
| a |
考点:函数与方程的综合运用,函数最值的应用
专题:综合题,函数的性质及应用
分析:(1)由t=
+
平方得
=
t2-1,从而将函数f(x)换元为m(t),而m(t)的定义域即t=
+
的值域,平方后求其值域即可;
(2)由(1)知,通过讨论对称轴的位置可得最大值关于a的函数g(a);
(3)假设存在大于
的正实数a满足g(a)=g(
),分类讨论,即可得出结论.
| 1+x |
| 1-x |
| 1-x2 |
| 1 |
| 2 |
| 1+x |
| 1-x |
(2)由(1)知,通过讨论对称轴的位置可得最大值关于a的函数g(a);
(3)假设存在大于
| 2 |
| 1 |
| a |
解答:
解:(1)由题意得
,∴-1≤x≤1,∴函数f(x)的定义域为[-1,1].
t=
+
,由x∈[-1,1]得,t2∈[2,4],所以t的取值范围是[
,2].
又
=
t2-1,∴m(t)=
at2-t-a,t∈[
,2];
(2)由题意知g(a)即为函数m(t)=
at2-t-a,t∈[
,2]的最大值.
注意到直线t=
是抛物线m(t)=
at2-t-a的对称轴,分以下几种情况讨论:
①
≤
,即a≥
知m(t)=
at2-t-a在[
,2]上单调递增,∴g(a)=m(2)=a-2.
②当
<
<2时,
<a<
,g(a)=m(
)=-
-a.
③当
≥2,即0<a≤
时,g(a)=m(
)=-
∴g(a)=
;
(3)由(2)可得g(
)=
.
假设存在大于
的正实数a满足g(a)=g(
),则
<a<2时,a-2=-
-
,方程无解;
a≥2时,a-2=-
,a=2-
<2,不符合.
综上所述,不存在大于
的正实数a满足g(a)=g(
).
|
t=
| 1+x |
| 1-x |
| 2 |
又
| 1-x2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
(2)由题意知g(a)即为函数m(t)=
| 1 |
| 2 |
| 2 |
注意到直线t=
| 1 |
| a |
| 1 |
| 2 |
①
| 1 |
| a |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
②当
| 2 |
| 1 |
| a |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| a |
| 1 |
| 2a |
③当
| 1 |
| a |
| 1 |
| 2 |
| 2 |
| 2 |
∴g(a)=
|
(3)由(2)可得g(
| 1 |
| a |
|
假设存在大于
| 2 |
| 1 |
| a |
| 2 |
| a |
| 2 |
| 1 |
| a |
a≥2时,a-2=-
| 2 |
| 2 |
综上所述,不存在大于
| 2 |
| 1 |
| a |
点评:本题考查了求函数定义域的方法以及利用换元法求函数值域的方法,解题时要注意换元后函数的定义域的变化.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 在正四面体ABCD中,M,N分别是BC,AD中点.
在正四面体ABCD中,M,N分别是BC,AD中点. 已知函数y=
已知函数y=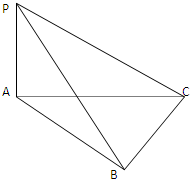 已知三棱锥P-ABC中,PA⊥平面ABC,∠ACB=90°,BC=1,AC=
已知三棱锥P-ABC中,PA⊥平面ABC,∠ACB=90°,BC=1,AC=