题目内容
3．
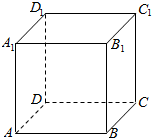（A类题）如图，在棱长为1的正方形ABCD-A1B1C1D1中选取四个点A1，C1，B，D，若A1，C1，B，D四个点都在同一球面上，则该球的表面积为3π．
分析 由题意，A1，C1，B，D四个点都在同一球面上，且为正方体的外接球，球的半径为$\frac{\sqrt{3}}{2}$，即可求出球的表面积．
解答 解：由题意，A1，C1，B，D四个点都在同一球面上，且为正方体的外接球，球的半径为$\frac{\sqrt{3}}{2}$，
∴球的表面积为$4π•\frac{3}{4}$=3π．
故答案为：3π．
点评 本题考查球的表面积，考查学生的计算能力，比较基础．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
13．已知椭圆$\frac{{x}^{2}}{49}$+$\frac{{y}^{2}}{24}$=1的左、右焦点分别为F1、F2，点A在椭圆上，且|AF2|=6，则△AF1F2的面积是（ ）
| A． | 48 | B． | 40 | C． | 32 | D． | 24 |
14．函数f（x）=$\frac{\sqrt{2-x}}{1-lo{g}_{2}x}$的定义域为（ ）
| A． | （0，2] | B． | （0，2） | C． | （-2，2） | D． | [-2，2] |
11．设X是离散型随机变量，其分布列为其中a≠0，b≠0，则$\frac{1}{a}$+$\frac{1}{b}$的最小值为8
| X | 0 | 1 | 2 |
| P | a | b | $\frac{1}{2}$ |
18．已知函数f（x）=sin（2x+φ）+cos（2x+φ）的图象与函数$g（x）=\sqrt{2}sin（{2x+\frac{π}{3}}）$的图象关于y轴对称，则φ的值可以为（ ）
| A． | $-\frac{7π}{12}$ | B． | $-\frac{5π}{12}$ | C． | $\frac{5π}{12}$ | D． | $\frac{7π}{12}$ |
8．若函数f（x）=$\left\{\begin{array}{l}{-x+6，x≤2}\\{3+lo{g}_{a}x，x＞2}\end{array}\right.$（a＞0且a≠1）的值域是[4，+∞），则实数a的取值范围是（ ）
| A． | （0，$\frac{1}{2}$） | B． | [$\frac{1}{2}$，1） | C． | （1，2） | D． | （1，2] |