题目内容
11.设X是离散型随机变量,其分布列为其中a≠0,b≠0,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为8| X | 0 | 1 | 2 |
| P | a | b | $\frac{1}{2}$ |
分析 由已知得a>0,b>0,a+b=$\frac{1}{2}$,由此利用基本不等式能求出$\frac{1}{a}$+$\frac{1}{b}$的最小值.
解答 解:∵X是离散型随机变量,a≠0,b≠0,
∴X的分布列性质得:$\left\{\begin{array}{l}{a+b=\frac{1}{2}}\\{a>0}\\{b>0}\end{array}\right.$
∴$\frac{1}{a}$+$\frac{1}{b}$=2($\frac{1}{a}$+$\frac{1}{b}$)(a+b)=2(2+$\frac{b}{a}$+$\frac{a}{b}$)≥2(2+2$\sqrt{\frac{b}{a}•\frac{a}{b}}$)=8,
当且仅当a=b=$\frac{1}{4}$时,取最小值,
∴$\frac{1}{a}$+$\frac{1}{b}$的最小值为8.
故答案为:8.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意离散型随机变量的分布列和基本不等式性质的合理运用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
16.设集合S={x|x>1},T={x||x-1|≤2},则(∁RS)∪T( )
| A. | (-∞,3] | B. | [-1,1] | C. | [-1,3] | D. | [-1,+∞) |
20.把1011011(2)转化成十进制数为( )
| A. | 88 | B. | 89 | C. | 90 | D. | 91 |
 一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8,.
一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8,.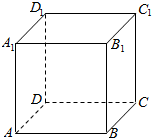 (A类题)如图,在棱长为1的正方形ABCD-A1B1C1D1中选取四个点A1,C1,B,D,若A1,C1,B,D四个点都在同一球面上,则该球的表面积为3π.
(A类题)如图,在棱长为1的正方形ABCD-A1B1C1D1中选取四个点A1,C1,B,D,若A1,C1,B,D四个点都在同一球面上,则该球的表面积为3π.