题目内容
15.自然对数的底数e=1+$\frac{1}{1}$+$\frac{1}{2×1}$+$\frac{1}{3×2×1}$+$\frac{1}{4×3×2×1}$+…+$\frac{1}{n×(n-1)×…×2×1}$,根据这个公式画出求e的近似值(n=100)的程序框图,并写出对应的程序.分析 由题意可得算法步骤为:第一步:使I=1;第二步:使S=2;第三步:使P=1;第四步:如果|S-2.718|>0.001判断为是,那么I←I+1,P←P×I,S←S+$\frac{1}{P}$,继续执行算法.否则,输出S,结束算法,结合算法步骤,利用循环结构能作出算法的程序框图,结合程序框图即可写出相应的程序代码.
解答 解:由题意可得算法步骤如下:
S1 I←1;
S2 S←2;
S3 P←1;
S4 如果|S-2.718|>0.001,那么I←I+1,P←P×I,S←S+$\frac{1}{P}$,重复S4;
S5 输出S.
流程图如下: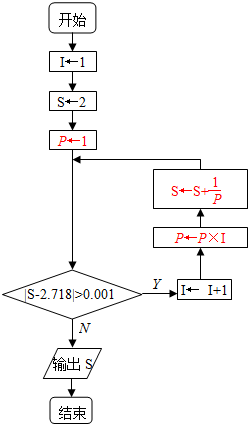
程序如下:
I=1
S=2
P=1
While|S-2.718|>0.001
I=I+1
P=P×I
S=S+$\frac{1}{P}$
End While
Print S
点评 本题考查设计算法的程序框图解决实际问题,是基础题.解题时要认真审题,注意熟练掌握循环结构的性质和应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.把1011011(2)转化成十进制数为( )
| A. | 88 | B. | 89 | C. | 90 | D. | 91 |
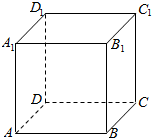 (A类题)如图,在棱长为1的正方形ABCD-A1B1C1D1中选取四个点A1,C1,B,D,若A1,C1,B,D四个点都在同一球面上,则该球的表面积为3π.
(A类题)如图,在棱长为1的正方形ABCD-A1B1C1D1中选取四个点A1,C1,B,D,若A1,C1,B,D四个点都在同一球面上,则该球的表面积为3π.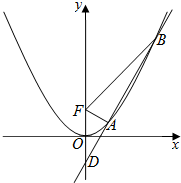 已知抛物线C:x2=4y的焦点为F,过点D(0,-1)的直线l与抛物线C交于不同的A、B两点.
已知抛物线C:x2=4y的焦点为F,过点D(0,-1)的直线l与抛物线C交于不同的A、B两点.