圆上的点到直线的距离最大值是.最小值是b.则＝( )A． B． C． D．题目和参考答案——青夏教育精英家教网—

题目内容

圆上的点到直线的距离最大值是，最小值是b，则＝(　　)

A．

B．

C．

D．

解析试题分析：把圆化为标准方程，∵圆心（1,1）到直线的距离为，∴a=d+r=，b=d-r，∴＝，故选B
考点：本题考查了直线与圆的位置关系
点评：到圆上一点距离的最值问题总是转化为到圆心距离的最值问题，设圆外一点P，则P到圆心为O、半径为r上动点的距离为d，有

练习册系列答案

相关题目

直线与圆的位置关系是（）

能够使圆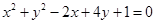上恰有两点到直线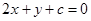距离等于1的的一个值为 ( )

当曲线y=与直线kx-y-2k+3=0有两个相异的交点时，实数k的取值范围是 ( )

如果圆x²+y²+Dx+Ey+F=0与x轴切于原点, 那么（）

A．D=0,E≠0, F≠0;	B．E=F=0,D≠0;
C．D="F=0," E≠0;	D．D=E=0,F≠0;

已知圆的方程为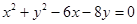.设该圆过点H（3，5）的两条弦分别为AC和BD，且.则四边形ABCD的面积最大值为（）

圆与直线没有公共点的充分不必要条件是( )

A．	B．
C．	D．

已知圆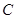与直线都相切，圆心在直线上，则圆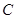的方程为（）

A．	B．
C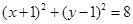．	D．

若直线3x＋y＋a＝0过圆x²＋y²＋2x－4y＝0的圆心，则a的值为( )

试题分类