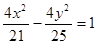题目内容
已知圆的方程为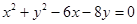 .设该圆过点H(3,5)的两条弦分别为AC和BD,且
.设该圆过点H(3,5)的两条弦分别为AC和BD,且 .则四边形ABCD的面积最大值为( )
.则四边形ABCD的面积最大值为( )
A. | B. | C.49 | D.50 |
C
解析试题分析:圆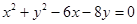 的圆心
的圆心 半径
半径 ,设
,设 ,所以四边形ABCD的面积
,所以四边形ABCD的面积 ,
, ,当且仅当
,当且仅当 即
即 时等号成立,所以面积最大为49
时等号成立,所以面积最大为49
考点:直线和圆相交及均值不等式
点评:本题求最值借助了均值不等式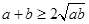 ,直线与圆相交时,圆心到直线的距离,圆的半径及弦长的一半构成直角三角形
,直线与圆相交时,圆心到直线的距离,圆的半径及弦长的一半构成直角三角形

练习册系列答案
相关题目
已知圆C经过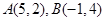
 两点,圆心在x轴上,则圆C的方程是
两点,圆心在x轴上,则圆C的方程是
A.  | B.  |
C.  | D. |
在平面直角坐标系 中,直线
中,直线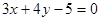 与圆
与圆 相交于
相交于 、
、 两点,则弦
两点,则弦 的长等于( )
的长等于( )
A.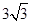 | B. | C. | D. |
直线 被圆
被圆 截得的线段的长为( )
截得的线段的长为( )
| A.2 | B. | C. | D.1 |
圆 上的点到直线
上的点到直线 的距离最大值是
的距离最大值是 ,最小值是b,则
,最小值是b,则 =( )
=( )
A. | B. | C. | D. |
已知圆的方程为(x-3)2+y2=9,则圆心坐标为( )
| A.(3,0) | B.(-3,0) | C.(0,3) | D.(0,-3) |
圆 和
和 的位置关系是( )
的位置关系是( )
| A.相离 | B.外切 | C.相交 | D.内切 |
已知 为圆
为圆 内异于圆心的一点,则直线
内异于圆心的一点,则直线 与该圆的位置关系是 ( )
与该圆的位置关系是 ( )
| A.相切 | B.相交 | C.相离 | D.相切或相交 |
 的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).
的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( ).