题目内容
能够使圆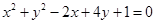 上恰有两点到直线
上恰有两点到直线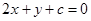 距离等于1的
距离等于1的 的一个值为 ( )
的一个值为 ( )
A. | B. | C. | D. |
A
解析试题分析:
圆的方程可化为:(x-1)2+(y+2)2=4,所以圆心M(1,-2),半径r=2,
结合图形容易知道,当且仅当M到直线l:2x+y+c=0的距离d∈(1,3)时,⊙M上恰有两个点到直线l的距离等于1,
由d=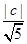 ∈(1,3)得:c∈(-3
∈(1,3)得:c∈(-3 ,-
,- )∪(
)∪( ,3
,3 ),而
),而 <3<3
<3<3 ,所以满足题意的c可以是3.
,所以满足题意的c可以是3.
故选A。
考点:直线与圆的位置关系。
点评:中档题,研究直线与圆的位置关系问题,往往利用数形结合法,应用“几何法”加以探究。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线 与圆
与圆 相交于
相交于 、
、 两点,则
两点,则 的值为( )
的值为( )
A. | B. | C. | D.与 有关的数值 有关的数值 |
已知 , 点
, 点 是圆
是圆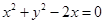 上的动点,则点M到直线AB的最大距离是
上的动点,则点M到直线AB的最大距离是
A. | B.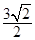 | C. | D. |
已知直线 :
: 和圆C:
和圆C:  ,则直线
,则直线 和圆C的位置关系为( ).
和圆C的位置关系为( ).
| A.相交 | B.相切 | C.相离 | D.不能确定 |
若关于 的方程组
的方程组 有实数解,则实数
有实数解,则实数 满足( )
满足( )
A. | B. | C. | D. |
在平面直角坐标系 中,直线
中,直线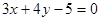 与圆
与圆 相交于
相交于 、
、 两点,则弦
两点,则弦 的长等于( )
的长等于( )
A.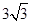 | B. | C. | D. |
圆O的方程为 ,圆M方程为
,圆M方程为 ,P为圆M上任一点,过P作圆O的切线PA,若PA与圆M的另一个交点为Q,当弦PQ的长度最大时,切线PA的斜率是( )
,P为圆M上任一点,过P作圆O的切线PA,若PA与圆M的另一个交点为Q,当弦PQ的长度最大时,切线PA的斜率是( )
| A.7或1 | B. 或1 或1 | C. 或-1 或-1 | D.7或-1 |
圆 上的点到直线
上的点到直线 的距离最大值是
的距离最大值是 ,最小值是b,则
,最小值是b,则 =( )
=( )
A. | B. | C. | D. |
若圆 的圆心到直线
的圆心到直线 的距离为
的距离为 ,则
,则 的值为( )
的值为( )
A. 或 或 | B. 或 或 | C. 或 或 | D. 或 或 |