题目内容
已知向量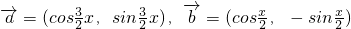 ,
, .
.
(1)求 ;
;
(2)求函数f(x)= 单调增区间.
单调增区间.
解:(1)∵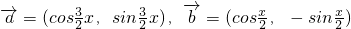
∴ =
= +2
+2 +
+ =2+2cos2x=4cos2x
=2+2cos2x=4cos2x
∵
∴cosx>0
∴ =2cosx;
=2cosx;
(2) =sin(
=sin( )=sinx
)=sinx
∴f(x)= =2sinx+2cosx=2
=2sinx+2cosx=2 sin(x+
sin(x+ )
)
其中 ,令μ=x+
,令μ=x+ ,则μ∈
,则μ∈ ,y=sinμ在
,y=sinμ在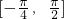 上为增函数
上为增函数
由 可得
可得 ,故sin(x+
,故sin(x+ )的增区间为
)的增区间为
即函数f(x)= 单调增区间为
单调增区间为
分析:(1)根据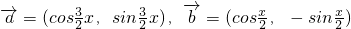 ,可得
,可得 =
= +2
+2 +
+ ,利用
,利用 ,即可求得
,即可求得 ;
;
(2)函数f(x)= =2sinx+2cosx=2
=2sinx+2cosx=2 sin(x+
sin(x+ ),
), ,令μ=x+
,令μ=x+ ,则可得μ的范围,y=sinμ在
,则可得μ的范围,y=sinμ在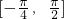 上为增函数,由此可得函数f(x)=
上为增函数,由此可得函数f(x)= 单调增区间.
单调增区间.
点评:本题考查向量知识的综合运用,考查向量的模,考查三角函数的单调性,解题的关键是利用三角函数知识求解.
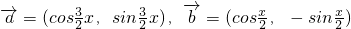
∴
 =
= +2
+2 +
+ =2+2cos2x=4cos2x
=2+2cos2x=4cos2x∵

∴cosx>0
∴
 =2cosx;
=2cosx;(2)
 =sin(
=sin( )=sinx
)=sinx∴f(x)=
 =2sinx+2cosx=2
=2sinx+2cosx=2 sin(x+
sin(x+ )
)其中
 ,令μ=x+
,令μ=x+ ,则μ∈
,则μ∈ ,y=sinμ在
,y=sinμ在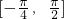 上为增函数
上为增函数由
 可得
可得 ,故sin(x+
,故sin(x+ )的增区间为
)的增区间为
即函数f(x)=
 单调增区间为
单调增区间为
分析:(1)根据
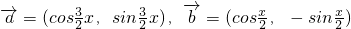 ,可得
,可得 =
= +2
+2 +
+ ,利用
,利用 ,即可求得
,即可求得 ;
;(2)函数f(x)=
 =2sinx+2cosx=2
=2sinx+2cosx=2 sin(x+
sin(x+ ),
), ,令μ=x+
,令μ=x+ ,则可得μ的范围,y=sinμ在
,则可得μ的范围,y=sinμ在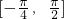 上为增函数,由此可得函数f(x)=
上为增函数,由此可得函数f(x)= 单调增区间.
单调增区间.点评:本题考查向量知识的综合运用,考查向量的模,考查三角函数的单调性,解题的关键是利用三角函数知识求解.

练习册系列答案
相关题目





 =
= ,
, ,
,
 ,若(∁RA)∪(∁RB)=∅,求实数a的取值范围.
,若(∁RA)∪(∁RB)=∅,求实数a的取值范围. 设函数
设函数
 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;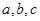 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 △ABC的面积为
△ABC的面积为 ,求
,求 的值.
的值. 中,已知向量
中,已知向量 且
且 .
. 与
与 之间的关系式;
之间的关系式; ,求四边形
,求四边形 的面积.
的面积. ,且
,且
 的解析式和它的最小正周期;
的解析式和它的最小正周期; 的值域。
的值域。