题目内容
已知向量 =
= ,
, ,
,
(1)求函数g(x)的解析式.
(2)若集合M={f(x)|f(x)+f(x+2)=f(x+1),x∈R},试判断g(x)与集合M的关系.
(3)记A={x|a≥2g(x)},
 ,若(∁RA)∪(∁RB)=∅,求实数a的取值范围.
,若(∁RA)∪(∁RB)=∅,求实数a的取值范围.
【答案】分析:(1)直接代入向量的数量积计算公式整理后即可求出函数g(x)的解析式;
(2)直接计算g(x)+g(x+2)看是否符合集合M中的元素所满足的条件即可得出结论;
(3)直接利用(CRA)∪(CRB)=∅,得到A=B=R;再分别利用A=R以及B=R求出对应的实数a的取值范围,综合即可得出结论.
解答:解:(1)∵向量 =
= ,
, ,
,
∴
=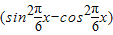
 ,(4分)
,(4分)
(2)∵
=
=
= ,
,
∴g(x)∈M.(8分)
(3)∵(CRA)∪(CRB)=∅,
∴A=B=R.
由A=R⇒a≥2 ①
由B=R⇒1<a≤5 ②.
由①,②得a∈[2,5](14分)
点评:本题主要考查平面向量数量积的运算以及元素与集合关系的判断.元素与集合之间的关系命题方向有二,一是验证元素是否是集合的元素;二是知元素是集合的元素,根据集合的属性求出相关的参数.
(2)直接计算g(x)+g(x+2)看是否符合集合M中的元素所满足的条件即可得出结论;
(3)直接利用(CRA)∪(CRB)=∅,得到A=B=R;再分别利用A=R以及B=R求出对应的实数a的取值范围,综合即可得出结论.
解答:解:(1)∵向量
 =
= ,
, ,
,
∴

=
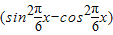
 ,(4分)
,(4分)(2)∵

=

=

=
 ,
,∴g(x)∈M.(8分)
(3)∵(CRA)∪(CRB)=∅,
∴A=B=R.
由A=R⇒a≥2 ①
由B=R⇒1<a≤5 ②.
由①,②得a∈[2,5](14分)
点评:本题主要考查平面向量数量积的运算以及元素与集合关系的判断.元素与集合之间的关系命题方向有二,一是验证元素是否是集合的元素;二是知元素是集合的元素,根据集合的属性求出相关的参数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目