题目内容
已知抛物线
(1)若 求该抛物线与
求该抛物线与 轴公共点的坐标;
轴公共点的坐标;
(2)若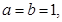 且当
且当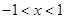 时,抛物线与
时,抛物线与 轴有且只有一个公共点,求c的取值范围;
轴有且只有一个公共点,求c的取值范围;
(3)若 且
且 时,
时, 时,
时, 试判断当
试判断当 时,抛物线与
时,抛物线与 轴是否有公共点?若有,请证明你的结论;若没有,说明理由.
轴是否有公共点?若有,请证明你的结论;若没有,说明理由.
(1)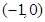 和
和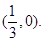 (2)当
(2)当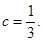 或
或 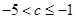 时,抛物线在
时,抛物线在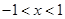 时与
时与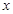 轴有且只有一个公共点. (3)当
轴有且只有一个公共点. (3)当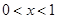 时,抛物线与
时,抛物线与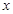 轴有两个公共点.
轴有两个公共点.
【解析】本题考查了求二次函数的解析式等相关的知识,同时还渗透了分类讨论的数学思想,是一道不错的二次函数综合题.
(1)将a、b、c的值代入抛物线后求得解析式,令y=0求出x的值就是交点坐标的横坐标;
(2)根据其在此范围内有一个交点,此时将两个值代入,分别大于零和小于零,进而求出相应的取值范围.
(3)因为由题意可得,当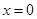 时,
时,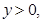 即
即 当
当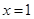 时,
时,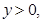
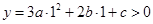
结合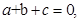 可得
可得 ,
,
因为 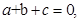
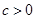 ,所以
,所以 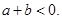 分析得到a,b的符号,然后结合判别式判定交点问题。
分析得到a,b的符号,然后结合判别式判定交点问题。
解:(1)当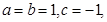 抛物线
抛物线 为
为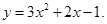
令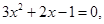 解得,
解得,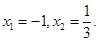
所以,抛物线 与
与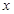 轴的公共点的坐标为
轴的公共点的坐标为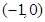 和
和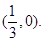 ……2分
……2分
(2)当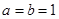 时,抛物线
时,抛物线 为
为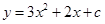 .
.
令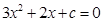 ,解之,得
,解之,得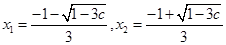 .
.
①若抛物线与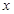 轴只有一个公共点,由题意,
轴只有一个公共点,由题意,
可得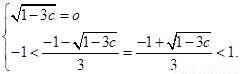 解之,得
解之,得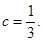
②若抛物线与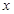 轴有两个公共点,由题意,可得
轴有两个公共点,由题意,可得
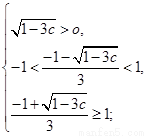 或
或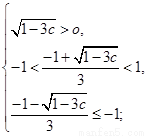
所以,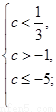 或
或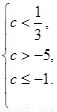 故
故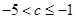 .
.
综上所述,当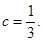 或
或 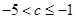 时,
时,
抛物线在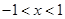 时与
时与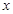 轴有且只有一个公共点.
……..8分
轴有且只有一个公共点.
……..8分
(3)由题意可得,当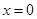 时,
时,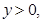 即
即 当
当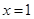 时,
时,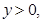
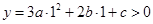
结合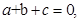 可得
可得 ,
,
因为 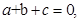
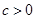 ,所以
,所以 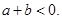
又  , 所以
, 所以
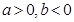 ……10分
……10分
令 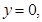 即
即 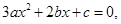 所以,此方程的判别式为
所以,此方程的判别式为 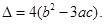
因为 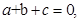 所以
所以 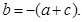 所以
所以 
因为 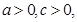 所以
所以 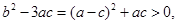 故
故 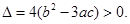
所以
抛物线与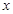 轴有且只有两个不同的交点.
……….13分
轴有且只有两个不同的交点.
……….13分
因为, 所以抛物线
所以抛物线 的顶点的纵坐标小于零。
的顶点的纵坐标小于零。
因为 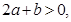
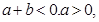 所以
所以 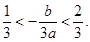
因为 抛物线的对称轴为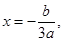 所以
所以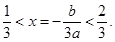
又当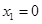 时,
时,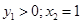 时,
时,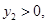 所以当
所以当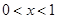 时,
时,
抛物线与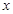 轴有两个公共点.
……16分
轴有两个公共点.
……16分

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案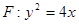
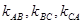 ,若A的坐标在原点,求
,若A的坐标在原点,求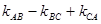 的值;
的值;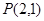 为顶点、其余各顶点均为抛物线F上的动点的多边形,写出各多边形各边所在的直线斜率之间的关系式,并说明理由
为顶点、其余各顶点均为抛物线F上的动点的多边形,写出各多边形各边所在的直线斜率之间的关系式,并说明理由