题目内容
20.已知实数列{an}是等比数列,其中a 7=1,且a 4,a 5+1,a 6成等差数列.(Ⅰ)求数列{ an }的通项公式;
(Ⅱ)数列{ an }的前n项和记为Sn,证明:Sn<128(n=1,2,3…).
解:(Ⅰ)设等比数列{ an }的公比为q(q![]() R),
R),
由a 7=a 1q6=1,得a1=q-6,从而a 4=a 1q3=q-3,a 5=a 1q4=q-2,a 6=a 1q5=q-1.
因为a 4,a 5+1,a 6成等差数列,所以a 4+a 6=2(a 5+1),
即q-3+q-1=2(q-2+1), q-1(q-2+1)=2(q-2+1).
所以q=![]() , 故
, 故![]() =64(
=64(![]() )n-1.
)n-1.
(Ⅱ)Sn=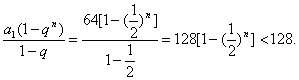

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目