题目内容
已知
(1)当 时,求
时,求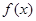 的极值;
的极值;
(2)当 时,讨论
时,讨论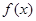 的单调性;
的单调性;
(3)若对任意的 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)极大值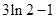 ,极小值1;(2)参考解析;(3)
,极小值1;(2)参考解析;(3)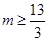
解析试题分析:(1)由已知 ,求函数
,求函数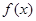 导函数,又
导函数,又 .即可得到函数
.即可得到函数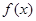 的极值点,从而求得极值.
的极值点,从而求得极值.
(2)当 时,
时, 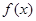 的导数为零时,得到两个零点
的导数为零时,得到两个零点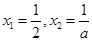 .所以要讨论
.所以要讨论 的大小,从而确定函数
的大小,从而确定函数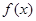 的单调性.
的单调性.
(3)因为对任意的 ,恒有
,恒有 成立.即求出
成立.即求出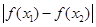 的最大值
的最大值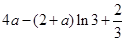 .所以
.所以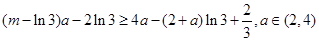 恒成立.再利用分离变量,即可得结论.
恒成立.再利用分离变量,即可得结论.
试题解析:(1)当a=1时可知 在
在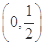 上是增函数,在
上是增函数,在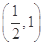 上是减函数. 在
上是减函数. 在  上是增函数
上是增函数
∴ 的极大值为
的极大值为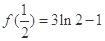 ,
, 的极小值.
的极小值.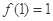

①当 时,
时, 在
在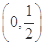 和
和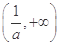 上是增函数,在
上是增函数,在 上是减函数
上是减函数
②当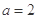 时,
时, 在
在 上是增函数;
上是增函数;
③当 时,
时, 在
在 和
和 上是增函数,在
上是增函数,在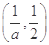 上是减函数
上是减函数
(3)当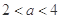 时,由(2)可知
时,由(2)可知 在
在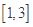 上是增函数,
上是增函数,
∴ 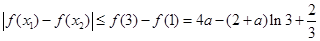
由 对任意的a∈(2, 4),x1, x2∈[1, 3]恒成立,
对任意的a∈(2, 4),x1, x2∈[1, 3]恒成立,
∴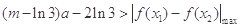
即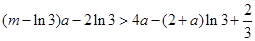 对任意
对任意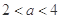 恒成立,
恒成立,
即 对任意
对任意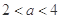 恒成立,
恒成立,
由于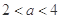 ,∴
,∴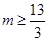 .
.
考点:1.函数的极值.2.函数的单调性.3.函数恒成立的问题.4.构造新函数利用函数的最值解决恒成立的问题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 函数
函数 在
在 上是单调递减函数,
上是单调递减函数, 方程
方程 无实根,若“
无实根,若“ 或
或 ”为真,“
”为真,“ 的取值范围。
的取值范围。 ,(
,( ).
). 有最值,求实数
有最值,求实数 的取值范围;
的取值范围; 时,若存在
时,若存在 、
、
 ,使得曲线
,使得曲线 在
在 与
与 处的切线互相平行,求证:
处的切线互相平行,求证: .
. ,其中
,其中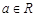 .
.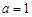 ,求函数
,求函数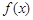 的极值点;
的极值点;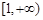 内单调递增,求实数
内单调递增,求实数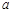 的取值范围.
的取值范围. .
.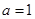 ,求曲线
,求曲线 在点
在点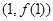 处的切线方程;
处的切线方程; 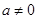 求函数
求函数 的单调区间.
的单调区间. -(2+a)lnx(a≥0).
-(2+a)lnx(a≥0).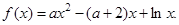
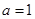 时,求曲线
时,求曲线 在点
在点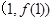 处的切线方程;
处的切线方程; 时,若
时,若 在区间
在区间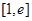 上的最小值为-2,求
上的最小值为-2,求 的取值范围;
的取值范围; 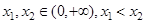 ,且
,且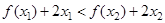 恒成立,求
恒成立,求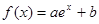 在
在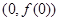 处切线为
处切线为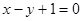 .
.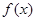 的解析式;
的解析式;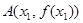 ,
,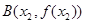 ,
,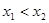 ,
,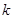 表示直线
表示直线 的斜率,求证:
的斜率,求证: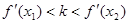 .
. .
. 的最小值;
的最小值;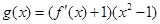 ,试问函数
,试问函数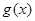 在
在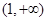 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.