题目内容
10.设f(x)是定义在(0,+∞)上的函数,对x,y∈(0,+∞)恒有f(x•y)=f(x)•f(y),f(x)>0,且当x>1时,f(x)>1.求证:f(x)在(0,+∞)上是增函数.分析 利用函数单调性的定义即可证明f(x)在(0,+∞)上是增函数.
解答 证明:任取x1,x2∈(0,+∞),且x1<x2,则$\frac{{x}_{2}}{{x}_{1}}$>1,
∵当x>1时,f(x)>1,
∴f($\frac{{x}_{2}}{{x}_{1}}$)>1
∵对x,y∈(0,+∞)恒有f(x•y)=f(x)•f(y),f(x)>0,
∴f(x2)=f($\frac{{x}_{2}}{{x}_{1}}$•x1)=f($\frac{{x}_{2}}{{x}_{1}}$)f(x1)>f(x1),
∴f(x2)>f(x1),
∴f(x)在定义域内是增函数.
点评 本题考查了抽象函数的应用,考查了函数的单调性的判断与证明,考查了学生灵活处理问题和解决问题的能力,属中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
20.一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归方程为$\hat y$=7.19x+73.93,则下列正确的叙述是( )
| A. | 10岁时身高一定是145.83cm | B. | 每长大一岁身高就增高73.93cm | ||
| C. | 每长大一岁身高就增高81.12cm | D. | 10岁时身高在145.83cm左右 |
1.在边长为1的等边△ABC中,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,$\overrightarrow{AB}$=$\overrightarrow{c}$,则$\overrightarrow{a}$•$\overrightarrow{b}$-$\overrightarrow{b}$•$\overrightarrow{c}$+$\overrightarrow{c}$•$\overrightarrow{a}$=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
18.已知两个等差数列{an}和{bn}的前n项和分别为Sn和Tn,且对一切正整数n都有$\frac{{S}_{n}}{{T}_{n}}$=$\frac{5n+3}{2n+7}$,则$\frac{{a}_{9}}{{b}_{9}}$的值为( )
| A. | $\frac{5}{2}$ | B. | $\frac{88}{41}$ | C. | $\frac{28}{17}$ | D. | $\frac{48}{25}$ |
5.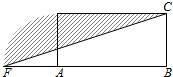 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )| A. | (4π+8)cm2 | B. | (4π+16)cm2 | C. | (3π+8)cm2 | D. | (3π+16)cm2 |
20.已知1ogm27•1og94=6,则m的值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | $\sqrt{2}$ |