题目内容
如图,EP交圆于E、C两点,PD切圆于D,G为CE上一点且 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
(1)求证:AB为圆的直径;
(2)若AC=BD,求证:AB=ED.
(1)详见解析;(2)详见解析
解析试题分析:(1)要证明 为圆的直径,只需证明
为圆的直径,只需证明 ,结合
,结合 ,在
,在 和
和 中,只需证明
中,只需证明 ,从而转化为证明
,从而转化为证明 ,由弦切角定理以及
,由弦切角定理以及 很容易证明;(2)要证明
很容易证明;(2)要证明 ,由(1)得,只需证明
,由(1)得,只需证明 为圆的直径.连接
为圆的直径.连接 ,只需证明
,只需证明 .只需证明
.只需证明 .因为
.因为 ,故
,故 ,根据同弧所对的圆周角相等得
,根据同弧所对的圆周角相等得 ,故
,故 ,从而.得证
,从而.得证
(1)因为 .所以
.所以 .由于
.由于 为切线,所以
为切线,所以 .又由于
.又由于 ,所以
,所以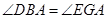 .由于
.由于 ,所以
,所以 ,
, .故
.故 为圆的直径.
为圆的直径.
(2)连接 .由于
.由于 是直径,故
是直径,故 .在
.在 和
和 中,
中, ,
, .从而
.从而 .于是
.于是 .又因为
.又因为 ,所以
,所以 .又因为
.又因为 ,所以
,所以 .故
.故 .由于
.由于 ,所以
,所以 ,
, 为直角.于是
为直角.于是 为直径.由(1)得,
为直径.由(1)得, .
.
考点:1、三角形全等;2、弦切角定理;3、圆的性质.

练习册系列答案
相关题目
 的两根,
的两根, 与△ABC开始时完全重合,然后让△ABC固定不动,将
与△ABC开始时完全重合,然后让△ABC固定不动,将 平方厘米?
平方厘米?
 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F. .
.
 AC,BD=
AC,BD=
 ,
, 分别为
分别为 的边
的边 ,
, 上的点,且不与
上的点,且不与 的长为
的长为 ,AC的长为n,
,AC的长为n, ,
, 的方程
的方程 的两个根。
的两个根。
 ,
, ,
, ,且
,且 ,求
,求 与⊙O的交点.若
与⊙O的交点.若 ,
, ,求证:
,求证: .
.

 和
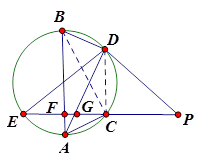
和 相交于A、B两点,过A点作
相交于A、B两点,过A点作

 则
则 ____________.
____________.