Question

已知和相交于A、B两点，过A点作切线交于点E，连接EB并延长交于点C，直线CA交于点D，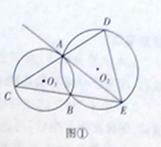
  
（1）当点D与点A不重合时（如图1），证明：ED²=EB·EC;
（2）当点D与点A重合时（如图2），若BC=2，BE=6，求的直径长.

Answer 1

（1）证明详见解析；(2)

解析试题分析：（1）连接AB，在EA的延长线上取点F，由弦切角定理可得∠FAC＝∠ABC，而∠FAC＝∠DAE，（对顶角）证得∠ABC＝∠DAE,然后内接四边形的性质证得∠ABC＝∠ADE,即得∠DAE＝∠ADE.所以EA＝ED,由切割线定理可得，即.
(2)直线CA与⊙O₂只有一个公共点，所以直线CA与⊙O₂相切，由弦切角定理知：然后证明，即AC与AE分别为⊙O₁和⊙O₂的直径．最后根据切割线定理证得AE的长.
试题解析：(1)连接AB，在EA的延长线上取点F，如图①所示．
∵AE是⊙O₁的切线，切点为A，
∴∠FAC＝∠ABC,.∵∠FAC＝∠DAE，
∴∠ABC＝∠DAE,∵∠ABC是⊙O₂内接四边形ABED的外角，
∴∠ABC＝∠ADE,∴∠DAE＝∠ADE.∴EA＝ED,∵,∴

(2)当点D与点A重合时，直线CA与⊙O₂只有一个公共点，
所以直线CA与⊙O₂相切．如图②所示，由弦切角定理知：


∴AC与AE分别为⊙O₁和⊙O₂的直径．    8分
∴由切割线定理知：EA²＝BE·CE，而CB＝2，BE＝6，CE=8
∴EA²＝6×8＝48，AE＝.故⊙O₂的直径为.      10分
考点：1.弦切角定理；2. 切割线定理;