题目内容
已知命题p:“∀x∈[1,2],x2-a≥0”,命题q:“∃x0∈R,x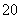 +2ax0+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围.
+2ax0+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围.
∵“p且q”是真命题,
∴p为真命题,q也为真命题.
若p为真命题,∵x∈[1,2]时,a≤x2恒成立,
∴a≤1.
若q为真命题,即x2+2ax+2-a=0有实根,Δ=4a2-4(2-a)≥0,
∴a≥1或a≤-2,
综上知所求实数a的取值范围是a≤-2或a=1.

练习册系列答案
相关题目
题目内容
已知命题p:“∀x∈[1,2],x2-a≥0”,命题q:“∃x0∈R,x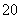 +2ax0+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围.
+2ax0+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围.
∵“p且q”是真命题,
∴p为真命题,q也为真命题.
若p为真命题,∵x∈[1,2]时,a≤x2恒成立,
∴a≤1.
若q为真命题,即x2+2ax+2-a=0有实根,Δ=4a2-4(2-a)≥0,
∴a≥1或a≤-2,
综上知所求实数a的取值范围是a≤-2或a=1.
