题目内容
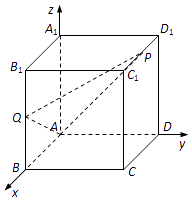
【题目】如图,在直三棱柱![]() (侧棱垂直于底面)中,
(侧棱垂直于底面)中,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() 使
使![]() 平面
平面![]() ?若存在,请确定点
?若存在,请确定点![]() 的位置;若不存在,也请说明理由.
的位置;若不存在,也请说明理由.
【答案】(1)证明见解析;(2)![]() 为
为![]() 的中点.
的中点.
【解析】
(1)由几何体的结构特征和线面垂直的判定定理,证得![]() 平面
平面![]() ,得到
,得到![]() ,进而得到
,进而得到![]() ,再由四边形
,再由四边形![]() 为正方形,所以
为正方形,所以![]() ,最后利用线面垂直的判定定理,即可证得
,最后利用线面垂直的判定定理,即可证得![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,分别连接
,分别连接![]() ,
,![]() ,
,![]() ,利用几何体的结构特征和线面平行的判定和性质,即可求解.
,利用几何体的结构特征和线面平行的判定和性质,即可求解.
(1)由题意,三棱柱![]() 为直三棱柱,所以
为直三棱柱,所以![]() ,
,
又因为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
又因为![]() ,所以四边形
,所以四边形![]() 为正方形,所以
为正方形,所以![]() .
.
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)当点![]() 为
为![]() 的中点时,
的中点时,![]() 平面
平面![]() .
.
证明如下:取![]() 的中点
的中点![]() ,分别连接
,分别连接![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() ,
,![]() 分别是直三棱柱
分别是直三棱柱![]() 侧棱
侧棱![]() ,
,![]() 的中点,所以
的中点,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.


【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)已知一续保人本年度的保费高于基本保费,求其保费比基本保费高出![]() 的概率.
的概率.
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:
组别 | PM2.5浓度 | 频数(天) | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
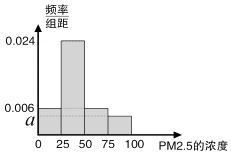
(1)将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图. ①求图4中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
(2)将频率视为概率,对于2016年的某3天,记这3天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为X,求X的分布列和数学期望.