题目内容
【题目】已知数列![]() 的首项为1,且
的首项为1,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,对任意
,对任意![]() ,都有
,都有![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .若对任意的
.若对任意的![]() ,不等式
,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
试题(1)由![]() ,得
,得![]() ,又
,又![]() ,两式相减得
,两式相减得![]() ,整理得
,整理得![]() ,即
,即![]() ,又因为
,又因为![]() ,
,![]() ,
,
利用累积法得![]() ,
,
从而可求出数学![]() 的通项公式为
的通项公式为![]() ;
;
在数列![]() 中,由
中,由![]() ,得
,得![]() ,且
,且![]() ,
,
所以数学![]() 是以首项为
是以首项为![]() ,公比为
,公比为![]() 的等比数列,从而数列
的等比数列,从而数列![]() 的通项公式为
的通项公式为![]() .
.
(2)由题意得![]() ,
,
![]() ,
,
两式相减得![]()
![]() ,
,
由等比数列前![]() 项和公式可求得
项和公式可求得![]() ,
,
由不等式![]() 恒成立,得
恒成立,得![]() 恒成立,
恒成立,
即![]() (
(![]() )恒成立,
)恒成立,
构造函数![]() (
(![]() ),
),
当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 不满足条件;
不满足条件;
当![]() 时,由二次函数性质知不恒成立;
时,由二次函数性质知不恒成立;
当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 满足条件.
满足条件.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:(1)∵![]() ,∴
,∴![]() (
(![]() ),两式相减得,
),两式相减得,![]() ,
,
∴![]() ,即
,即![]() (
(![]() ),又因为
),又因为![]() ,
,![]() ,从而
,从而![]()
∴![]() (
(![]() ),
),
故数列![]() 的通项公式
的通项公式![]() (
(![]() ).
).
在数列![]() 中,由
中,由![]() ,知数列
,知数列![]() 是等比数列,首项、公比均为
是等比数列,首项、公比均为![]() ,
,
∴数列![]() 的通项公式
的通项公式![]() .
.
(2)∴![]() ①
①
∴![]() ②
②
由①-②,得![]()
![]() ,
,
∴![]() ,
,
不等式![]() 即为
即为![]() ,
,
即![]() (
(![]() )恒成立.
)恒成立.
方法一、设![]() (
(![]() ),
),
当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 不满足条件;
不满足条件;
当![]() 时,由二次函数性质知不恒成立;
时,由二次函数性质知不恒成立;
当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 满足条件.
满足条件.
综上所述,实数λ的取值范围是![]() .
.
方法二、也即![]() (
(![]() )恒成立,
)恒成立,
令![]() .则
.则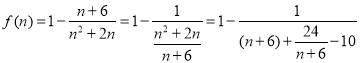 ,
,
由![]() ,
,![]() 单调递增且大于0,∴
单调递增且大于0,∴![]() 单调递增∴
单调递增∴![]()
∴实数λ的取值范围是![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目