题目内容
对于函数 (
( ).
).
(1)探索并证明函数 的单调性;
的单调性;
(2)是否存在实数 使函数
使函数 为奇函数?若有,求出实数
为奇函数?若有,求出实数 的值,并证明你的结论;若没有,说明理由.
的值,并证明你的结论;若没有,说明理由.
 (
( ).
).(1)探索并证明函数
 的单调性;
的单调性;(2)是否存在实数
 使函数
使函数 为奇函数?若有,求出实数
为奇函数?若有,求出实数 的值,并证明你的结论;若没有,说明理由.
的值,并证明你的结论;若没有,说明理由.(1)单调增;(2) .
.
 .
.试题分析:(1)直接利用增函数的定义证明;(2)法一:直接用定义
 ,可得
,可得 ,法二:先由
,法二:先由 求得
求得 ,再证明
,再证明 恒成立.
恒成立.试题解析:(1)任取
 ,且
,且 ,则
,则
 ,
, ,
,
 ,得
,得 在R上是增函数; (6分)
在R上是增函数; (6分)(2)由
 ,得
,得 ,
, ,又
,又
所以当
 时,
时, 为奇函数. (12分)
为奇函数. (12分)
练习册系列答案
相关题目
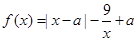 ,
,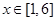 ,
,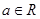 .
.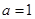 ,试判断并用定义证明函数
,试判断并用定义证明函数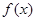 的单调性;
的单调性;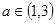 时,求证函数
时,求证函数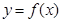 的定义域为
的定义域为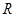 ,若存在常数
,若存在常数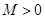 ,使
,使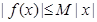 对一切
对一切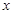 均成立,则称为“有界泛函”.现在给出如下
均成立,则称为“有界泛函”.现在给出如下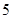 个函数:
个函数: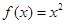 ; ②
; ②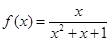 ;③
;③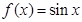 ;④
;④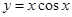 ;
;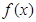 是
是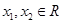 ,均有
,均有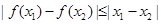 .
.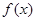 是定义在[-1,1]上的奇函数且
是定义在[-1,1]上的奇函数且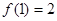 ,当
,当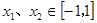 ,且
,且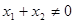 时,有
时,有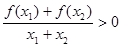 ,若
,若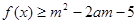 对所有
对所有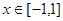 、
、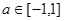 恒成立,则实数
恒成立,则实数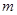 的取值范围是_________.
的取值范围是_________.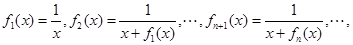 则函数
则函数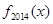 是( )
是( )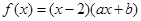 为偶函数,且在
为偶函数,且在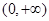 单调递增,则
单调递增,则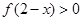 的解集为( )
的解集为( )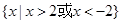
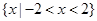
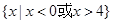
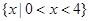
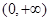 上单调递增的是( )
上单调递增的是( )