题目内容
设函数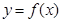 的定义域为
的定义域为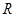 ,若存在常数
,若存在常数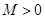 ,使
,使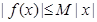 对一切
对一切
实数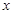 均成立,则称为“有界泛函”.现在给出如下
均成立,则称为“有界泛函”.现在给出如下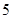 个函数:
个函数:
①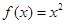 ; ②
; ②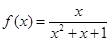 ;③
;③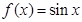 ;④
;④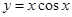 ;
;
⑤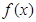 是
是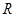 上的奇函数,且满足对一切
上的奇函数,且满足对一切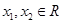 ,均有
,均有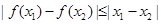 .
.
其中属于“有界泛函”的函数是 (填上所有正确的序号)
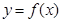 的定义域为
的定义域为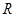 ,若存在常数
,若存在常数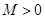 ,使
,使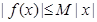 对一切
对一切实数
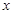 均成立,则称为“有界泛函”.现在给出如下
均成立,则称为“有界泛函”.现在给出如下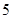 个函数:
个函数:①
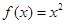 ; ②
; ②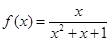 ;③
;③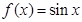 ;④
;④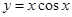 ;
;⑤
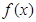 是
是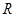 上的奇函数,且满足对一切
上的奇函数,且满足对一切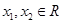 ,均有
,均有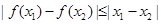 .
.其中属于“有界泛函”的函数是 (填上所有正确的序号)
②③④⑤
试题分析:根据题意,要满足“有界泛函”的定义,必须存在常数
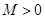 ,使得
,使得 的图像不在
的图像不在 的图像的上方,我们结合定义及函数解析式或图象特征来判断.
的图像的上方,我们结合定义及函数解析式或图象特征来判断.对于①,
 ,当
,当 时
时 ,故不选①;
,故不选①;对于②,函数
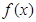 的定义域为
的定义域为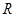 ,
, ,故②正确;
,故②正确;对于③,
 时由
时由 有
有 ,故
,故 ,故③正确;
,故③正确;对于④,
 ,故④正确;
,故④正确;对于⑤,令
 ,则
,则 ,已知式化为
,已知式化为 ,显然也符合定义.
,显然也符合定义.
练习册系列答案
相关题目
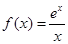 的定义域为
的定义域为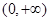 .
.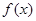 在
在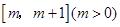 上的最小值;
上的最小值;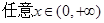 ,不等式
,不等式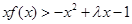 恒成立,求实数
恒成立,求实数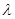 的取值范围.
的取值范围. (
( ).
). 的单调性;
的单调性; 使函数
使函数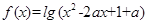 在区间(-∞,1]上递减,则a的取值范围为( )
在区间(-∞,1]上递减,则a的取值范围为( )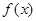 是定义在R上的偶函数,它在
是定义在R上的偶函数,它在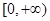 上是减函数. 则下列各式一定成
上是减函数. 则下列各式一定成
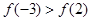
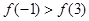
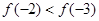
 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )



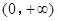 内单调递减,并且是偶函数的是( )
内单调递减,并且是偶函数的是( )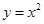
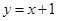
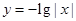
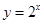
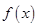 是
是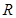 上的奇函数,且
上的奇函数,且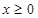 时,
时,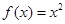 ,对任意
,对任意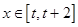 ,不等式
,不等式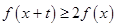 恒成立,则
恒成立,则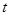 的取值范围( )
的取值范围( )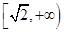
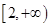

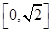
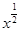 ,②y=
,②y=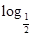 (x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )