题目内容
19．若过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）左焦点的直线与它的两个交点及其右焦点构成周长为16的三角形，此椭圆的离心率为0.5，求这个椭圆方程．分析 设左、右焦点分别为F，F'，两个交点为A，B，由椭圆的定义可得|AF|+|AF'|=|BF|+|BF'|=2a，则4a=16，运用离心率公式可得c=2，求得b，进而得到椭圆方程．
解答 解：设左、右焦点分别为F，F'，两个交点为A，B，
由椭圆的定义可得|AF|+|AF'|=|BF|+|BF'|=2a，
即有三角形的周长为4a=16，解得a=4，
由e=$\frac{c}{a}$=$\frac{1}{2}$，解得c=2，
b=$\sqrt{{a}^{2}-{c}^{2}}$=2$\sqrt{3}$，
则椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1．
点评 本题考查椭圆的方程的求法，注意运用椭圆的定义和基本量的关系，考查运算能力，属于基础题．
练习册系列答案
相关题目
在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=60°，AC=CC1=2，BC=1，E，F分别是A1C1，BC的中点．
7．近年来空气污染是生活中一个重要的话题，PM2.5就是空气质量的其中一个重要指标，各省、市、县均要进行实时监测．空气质量指数要求PM2.5 24小时浓度均值分：优、良、轻度污染、中度污染、重度污染、严重污染六级．如图是某市2015年某月30天的PM2.5 24小时浓度均值数据．
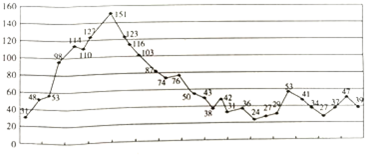
（Ⅰ）根据数据绘制频率分布表，并求PM2.5 24小时浓度均值的中位数；
（Ⅱ）专家建议，空气质量为优、良时可以正常进行某项户外体育活动，轻度污染及以上时，不宜进行该项户外体育活动．若以频率作为概率，用统计的结果分析，在2015年随机抽取6天，正常进行该项户外体育活动的天数与不宜进行该项户外体育活动的天数的差的绝对值为随机变量X，求X的分布列和数学期望．
（Ⅰ）根据数据绘制频率分布表，并求PM2.5 24小时浓度均值的中位数；
| 空气质量 指数类别 | 优 [0，35] | 良 （35，75] | 轻度污染 （75，115] | 中度污染 （115，150] | 重度污染 （150，250] | 严重污染 （250，500] | 合计 |
| 频数 | 30 | ||||||
| 频率 | 1 |
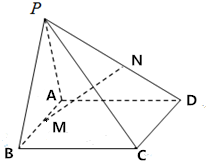如图，四棱锥P-ABCD中，△ABC与△PAB均为等边三角形，AC=$\sqrt{2}$AD=$\sqrt{2}$CD，PC=$\frac{3}{2}$AB．