题目内容
点P是曲线y=x2-lnx上任意一点,则点p到直线y=x-2的最小距离为( )
A、
| ||||
B、
| ||||
C、2
| ||||
| D、2 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的综合应用
分析:由题意知,当曲线上过点P的切线和直线y=x-2平行时,点P到直线y=x-2的距离最小.求出曲线对应的函数的导数,令导数值等于1,可得且点的坐标,此切点到直线y=x-2的距离即为所求.
解答:
解:点P是曲线y=x2-lnx上任意一点,
当过点P的切线和直线y=x-2平行时,点P到直线y=x-2的距离最小.
直线y=x-2的斜率等于1,
令y=x2-lnx的导数 y′=2x-
=1,x=1,或 x=-
(舍去),
故曲线y=x2-lnx上和直线y=x-2平行的切线经过的切点坐标(1,1),
点(1,1)到直线y=x-2的距离等于
,
故点P到直线y=x-2的最小距离为
,
故选:B.
当过点P的切线和直线y=x-2平行时,点P到直线y=x-2的距离最小.
直线y=x-2的斜率等于1,
令y=x2-lnx的导数 y′=2x-
| 1 |
| x |
| 1 |
| 2 |
故曲线y=x2-lnx上和直线y=x-2平行的切线经过的切点坐标(1,1),
点(1,1)到直线y=x-2的距离等于
| 2 |
故点P到直线y=x-2的最小距离为
| 2 |
故选:B.
点评:本题考查点到直线的距离公式的应用,函数的导数的求法及导数的意义,体现了转化的数学思想.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
已知复数z=-1+
i,则|z|=( )
| 3 |
| A、2 | ||
| B、3 | ||
| C、4 | ||
D、
|
方程ay=b2x2+c中的a,b,c∈{-2,-1,0,1,2,3,4},且a,b,c互不相同.在所有这些方程所表示的曲线中,不同的抛物线共有( )
| A、150条 | B、104条 |
| C、100条 | D、62条 |
已知方程|2x-1|=a有两个不等实根,则实数a的取值范围是( )
| A、(-∞,0) |
| B、(1,2) |
| C、(0,+∞) |
| D、(0,1) |
已知椭圆
+
=1的一个焦点为(2,0),则椭圆的方程是( )
| x2 |
| a2 |
| y2 |
| 2 |
A、
| ||||
B、
| ||||
C、x2+
| ||||
D、
|
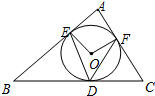 如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )| A、40° | B、55° |
| C、65° | D、70° |
若a-2i=b+ai,其中a、b∈R,i是虚数单位,则a+b=( )
| A、-4 | B、4 | C、0 | D、数值不定 |
 将连续整数1,2,…,25填入如图所示的5行5列的表格中,使每一行的数字从左到右都成递增数列,则第三列各数之和的最小值为
将连续整数1,2,…,25填入如图所示的5行5列的表格中,使每一行的数字从左到右都成递增数列,则第三列各数之和的最小值为