题目内容
设数列 满足
满足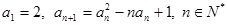 .
.
(1)求 ;
;
(2)由(1)猜想 的一个通项公式,并用数学归纳法证明你的结论;(本题满分13分)
的一个通项公式,并用数学归纳法证明你的结论;(本题满分13分)
(1) ,
, ,
, ;(2)见解析
;(2)见解析
解析试题分析:(1)根据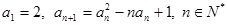 把
把 换成1、2、3即可得解。(2)由前面4项归纳得到
换成1、2、3即可得解。(2)由前面4项归纳得到 的通项公式,然后用数学归纳法来证明即可:
的通项公式,然后用数学归纳法来证明即可:
试题解析:(1)由 ,得
,得 2分
2分
由 ,得
,得 , 4分
, 4分
由 ,得
,得 6分
6分
(2)由(1)猜想 7分
7分
下面用数学归纳法证明
①当 时,
时,  ,猜想成立; 8分
,猜想成立; 8分
②假设 时,猜想成立,即
时,猜想成立,即 , 9分
, 9分
那么当 时,
时,
所以当 时,猜想也成立 12分
时,猜想也成立 12分
由①②知,对于任意 都有猜想成立 13分
都有猜想成立 13分
考点:数列与数学归纳法的综合

练习册系列答案
相关题目
 满足
满足 ,其中
,其中 ,设
,设 ,则
,则 等于 .
等于 .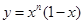 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为 ,则
,则 的前n项和是 .
的前n项和是 . 满足
满足 ,
, .
. ;
; 中,
中, ,其中
,其中 。
。 的值;
的值;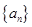 满足:
满足: .
.
 -100.
-100. 中各项均为正,有
中各项均为正,有 ,
, ,
, 中,
中, ,点
,点 在直线
在直线 上.
上. 和
和 的值;(2)求数列
的值;(2)求数列 和
和 ;
; ,求数列
,求数列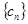 的前n项和
的前n项和 .
.