题目内容
设数列 满足
满足 ,
, .
.
(1)求 ;
;
(2)先猜想出 的一个通项公式,再用数学归纳法证明你的猜想.
的一个通项公式,再用数学归纳法证明你的猜想.
(1)5,7,9;(2)猜想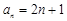 ;证明祥见解析.
;证明祥见解析.
解析试题分析:(1)由已知等式: 令n=1,再将
令n=1,再将 代入即可求得
代入即可求得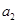 的值;再令n=2并将
的值;再令n=2并将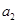 的值就可求得
的值就可求得 的值;最后再令n=2并将
的值;最后再令n=2并将 的值就可求得
的值就可求得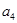 的值;(2)由已知及(1)的结果,可猜想出
的值;(2)由已知及(1)的结果,可猜想出 的一个通项公式;用数学归纳法证明时应注意格式:①验证
的一个通项公式;用数学归纳法证明时应注意格式:①验证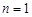 时猜想正确;②作归纳假设:假设当
时猜想正确;②作归纳假设:假设当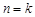 时,猜想成立,在此基础上来证明
时,猜想成立,在此基础上来证明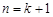 时猜想也成立,注意在此证明过程中要充分利用已知条件找出
时猜想也成立,注意在此证明过程中要充分利用已知条件找出 之间的关系,并一定要用到假设当
之间的关系,并一定要用到假设当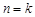 时的结论;最后一定要下结论.
时的结论;最后一定要下结论.
试题解析: (1)由条件 ,依次得
,依次得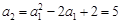 ,
,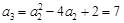 ,
,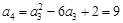 , 6分
, 6分
(2)由(1),猜想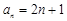 . 7分
. 7分
下用数学归纳法证明之:
①当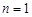 时,
时,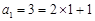 ,猜想成立; 8分
,猜想成立; 8分
②假设当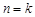 时,猜想成立,即有
时,猜想成立,即有 , 9分
, 9分
则当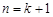 时,有
时,有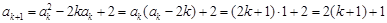 ,
,
即当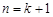 时猜想也成立, 13分
时猜想也成立, 13分
综合①②知,数列 通项公式为
通项公式为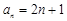 . 14分
. 14分
考点:1.数列的概念;2.归纳猜想;3.数学归纳法.

练习册系列答案
相关题目
 行有
行有 ,每个数是它下一行左右相邻两数的和,如:
,每个数是它下一行左右相邻两数的和,如: …,则第
…,则第 行第3个数字是
行第3个数字是 .(用含
.(用含 的式子作答)
的式子作答)
 是数列
是数列 的前
的前 项和,若
项和,若 ,则数列
,则数列 ,则
,则
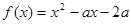 ,若存在
,若存在 ,使得
,使得 成立,则
成立,则
 中,
中, 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 则
则 的前n项和为
的前n项和为 则三点
则三点 共线;
共线; ”的否定是“
”的否定是“ ”;
”; 在(0,1)没有零点,则k的取值范围是
在(0,1)没有零点,则k的取值范围是
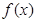 是定义在R上的奇函数,
是定义在R上的奇函数, 的解集为(
的解集为( 2,2)
2,2) 中,若
中,若 且
且 ,则数列
,则数列 ____________。
____________。 的前
的前 项和
项和 .
. 满足
满足 ,且
,且 ,求
,求 .
. 满足
满足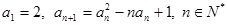 .
. ;
; 的一个通项公式,并用数学归纳法证明你的结论;(本题满分13分)
的一个通项公式,并用数学归纳法证明你的结论;(本题满分13分)
 ,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用
,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用 分别表示在第
分别表示在第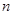 次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数. ,分别求出第二次,第三次选“音乐欣赏”课的人数
,分别求出第二次,第三次选“音乐欣赏”课的人数 ;
; 是等比数列,并用
是等比数列,并用 ;
; 满足
满足 (
( ).
). 的值;
的值; (用含
(用含 的式子表示);
的式子表示); ,求
,求