题目内容
设F1,F2为双曲线C:
-
=1(a>0,b>0)的左、右焦点,过坐标原点O的直线与双曲线C在第一象限内交于点P,若|PF1|+|PF2|=6a,且△PF1F2为锐角三角形,则直线OP斜率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(
| ||||||
B、(
| ||||||
C、(1,
| ||||||
D、(
|
考点:双曲线的简单性质
专题:圆锥曲线中的最值与范围问题
分析:首先,设直线OP的方程,然后根据双曲线的定义,并结合条件|PF1|+|PF2|=6a,求解|PF1|和|PF2|的值,然后,根据△PF1F2为锐角三角形,联立方程组写出相应的点P的坐标,最后限制范围即可.
解答:
解:∵|PF1|+|PF2|=6a,
|PF1|-|PF2|=2a,
∴|PF1|=4a,|PF2|=2a,
∵|F1F2|=2c,
∵△PF1F2为锐角三角形,
∴
,
∴
,
∴
<e<
,
∴3<1+(
)2<5,
∴
<
<2,
欲使得过坐标原点O的直线与双曲线C在第一象限内交于点P,
∴k∈(
,
).
故选:A.
|PF1|-|PF2|=2a,
∴|PF1|=4a,|PF2|=2a,
∵|F1F2|=2c,
∵△PF1F2为锐角三角形,
∴
|
∴
|
∴
| 3 |
| 5 |
∴3<1+(
| b |
| a |
∴
| 2 |
| b |
| a |
欲使得过坐标原点O的直线与双曲线C在第一象限内交于点P,
∴k∈(
2
| ||
| 3 |
| 4 |
| 3 |
故选:A.
点评:本题重点考查了双曲线的标准方程、几何性质、直线与双曲线的位置关系等知识,属于中档题.解题关键是理解直线与双曲线的位置关系处理思路和方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
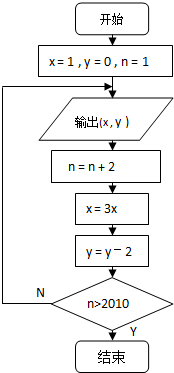 已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),…(xn,yn),…
已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),…(xn,yn),…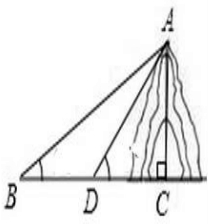 如图,从B处看山顶A的仰角为45°,向前100米,在D处看山顶A的仰角为60°,求:山AC的高度(已知sin15°=
如图,从B处看山顶A的仰角为45°,向前100米,在D处看山顶A的仰角为60°,求:山AC的高度(已知sin15°=