Question

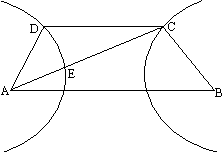
如下图,已知双曲线C₁的方程为=1(a＞0,b＞0),A、B为其左、右两个顶点,P是双曲线C₁上的任意一点,引QB⊥PB,QA⊥PA,AQ与BQ交于点Q.

(1)求Q点的轨迹方程;

(2)设(1)中所求轨迹为C₂,C₁、C₂的离心率分别为e₁、e₂,当e₁≥时,求e₂的取值范围.

Answer 1

(1)解法一:设P(x₀,y₀),Q(x,y),

∵A(-a,0),B(a,0),QB⊥PB,QA⊥PA,

∴

由（1）×（2）,得=1.                                              （3）

∵=1,∴.

代入（3）得b²y²=x²a²-a⁴,

即a²x²-b²y²=a⁴.

经检验点(-a,0)、(a,0)不合题意,

因此Q点的轨迹方程为a²x²-b²y²=a⁴〔除点(-a,0),(a,0)外〕.

解法二:设P(x₀,y₀),Q(x,y),

∵A(-a,0),B(a,0),QB⊥PB,QA⊥PA,

∴

∴

由（1）-（2）,得2ax₀=-2ax.

∴x₀=-x.                                                                     （3）

把（3）代入（2）可解得y₀=-.                  （4）

把（3）（4）代入=1,得=1.

∵当x=±a时,不合题意,

∴x²-a²≠0.∴a²x²-b²y²=a⁴.

∴Q点的轨迹方程为a²x²-b²y²=a⁴〔除点(-a,0),(a,0)外〕.

解法三:设P(x₀,y₀),Q(x,y),

∵PA⊥QA,∴=-1.                                                ①

连结PQ,取PQ中点R.

∵PA⊥QA,QB⊥PB,

∴|RA|=|PQ|,|RB|=|PQ|.

∴|RA|=|RB|.∴R点在y轴上.

∴=0,即x₀=-x.                                                        ②

把②代入①,得=-1.∴y₀=.                                      ③

把②③代入=1,得=1.

∵x=±a时,不合题意,∴x²-a²≠0.

整理得a²x²-b²y²=a⁴.

∴Q点的轨迹方程为a²x²-b²y²=a⁴〔除点(-a,0),(a,0)外〕.

(2)解:由(1)得C₂的方程为=1,

.

∵e₁≥,e₂²≤1+=2,∴1＜e₂≤.