题目内容
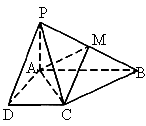
如下图所示,已知梯形ABCD中,|AB|=2|CD|,点E分有向线![]() 所成的比为λ,双曲线过C、D、E三点,且以A、B为焦点.当
所成的比为λ,双曲线过C、D、E三点,且以A、B为焦点.当![]() ≤λ≤
≤λ≤![]() 时,求双曲线离心率e的取值范围.
时,求双曲线离心率e的取值范围.
答案:
解析:
解析:
|
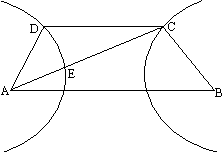
解析:以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系xOy,则CD⊥y轴.因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于y轴对称. 依题意,记A(-c,0),C( 由定比分点坐标公式得x0= 设双曲线的方程为 由点C、E在双曲线上,将点C、E的坐标和e=
由①式得 将③式代入②式,整理得 由题设 解得 所以双曲线的离心率e的取值范围为[ 点评:本题主要考查坐标法、定比分点坐标公式、双曲线的概念和性质以及推理、运算能力和综合应用数学知识解决问题的能力. |

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 =
=


 ,PA⊥底面ABCD,且
,PA⊥底面ABCD,且 ,M是PB的中点.
,M是PB的中点.
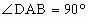 ,PA⊥底面ABCD,且
,PA⊥底面ABCD,且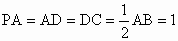 ,M是PB的中点.
,M是PB的中点.