题目内容
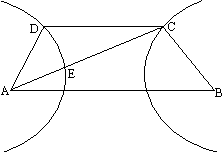
如下图,已知双曲线C的方程为
=1(a＞0,b＞0),过右焦点F作直线在第一、三象限的渐近线的垂线l,设垂足为P,且l与双曲线C的左、右支的交点分别为A、B. 
(1)求证:点P在双曲线C的右准线上;
(2)求双曲线C的离心率的取值范围.
(1)证明:设双曲线的右焦点为F(c,0),在第一、三象限的渐近线方程为y=
x,则直线l的方程为y=-(x-c).
解方程组
即P(
,
),
∴P点在右准线上.
(2)解:直线l与双曲线左、右支各交于一点.由图形知直线l:y=-
(x-c)与渐近线y=-
x相交于第二象限.
∴-
＞-
,即a2＜b2.
∴c2=a2+b2＞2a2.
∴e=
＞
.
练习册系列答案
阅读快车系列答案
相关题目
所成的比为λ，双曲线过C、D、E三点，且以A、B为焦点．当
≤λ≤
时，求双曲线离心率e的取值范围．
=1(a＞0,b＞0)的右焦点。P为双曲线C右支上一点，且位于x轴上方，M为左准线上一点，O为坐标原点。已知四边形OFPM为平行四边形，|PF|=λ|OF|.