题目内容
因为某种产品的两种原料相继提价，所以生产者决定对产品分两次提价，现在有三种提价方案：
方案甲：第一次提价p%，第二次提价q%；
方案乙：第一次提价q%，第二次提价p%；
方案丙：第一次提价
，第二次提价，
其中p＞q＞0，比较上述三种方案，提价最多的是
- A.甲
- B.乙
- C.丙
- D.一样多
C
分析：两次提价属于增长率问题，分别计算出方案甲，方案乙，方案丙增长后的价格，再比较大小．
解答：设提价前的价格为1，那么两次提价后的价格为，方案甲：（1+p%）（1+q%）=1+p%+q%+0.01pq%；
方案乙：（1+q%）（1+p%）=1+p%+q%+0.01pq%；
方案丙：（1+）（1+）=1+p%+q%+
=1+p%+q%+0.01×
%；
∵≥pq，且p＞q＞0，∴上式“=”不成立；所以，方案丙提价最多．
故应选：C．
点评：本题考查了增长率问题和基本不等式的应用，是基础题．
分析：两次提价属于增长率问题，分别计算出方案甲，方案乙，方案丙增长后的价格，再比较大小．
解答：设提价前的价格为1，那么两次提价后的价格为，方案甲：（1+p%）（1+q%）=1+p%+q%+0.01pq%；
方案乙：（1+q%）（1+p%）=1+p%+q%+0.01pq%；
方案丙：（1+
）（1+）=1+p%+q%+=1+p%+q%+0.01×%；∵
≥pq，且p＞q＞0，∴上式“=”不成立；所以，方案丙提价最多．故应选：C．
点评：本题考查了增长率问题和基本不等式的应用，是基础题．
练习册系列答案
53天天练系列答案
相关题目
、
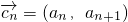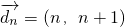（n=1，2，3，…，k-1），若
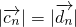，则满足条件的数列{an}的个数为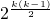
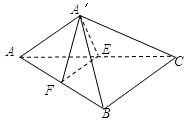如图，E、F分别为直角三角形ABC的直角边AC和斜边AB的中点，沿EF将△AEF折起到△A′EF的位置，连接A′B、A′C．
，AB=BC=2AD=2，E、F分别是线段AB、CD上的动点且EF∥BC，G是BC的中点．沿EF将梯形ABCD翻折，使平面AEFD丄平面EBCF （如图2）．
成等比数列，求
的取值范围．